过点 $C\left( {0,1} \right)$ 的椭圆 $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\left(a > b > 0\right)$ 的离心率为 $\dfrac{\sqrt 3 }{2}$,椭圆与 $x$ 轴交于两点 $A\left(a,0\right)$,$B\left( - a,0\right)$,过点 $C$ 的直线 $l$ 与椭圆交于另一点 $D$,并与 $x$ 轴交于点 $P$,直线 $AC$ 与直线 $BD$ 交于点 $Q$.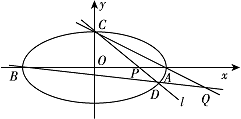

【难度】
【出处】
2011年高考四川卷(文)
【标注】
-
当直线 $l$ 过椭圆右焦点时,求线段 $CD$ 的长;标注答案略解析由已知得\[b = 1,\dfrac{c}{a} = \dfrac{\sqrt 3 }{2},\]解得\[a = 2,\]所以椭圆方程为\[\dfrac{x^2}{4} + {y^2} = 1.\]椭圆的右焦点为 $\left(\sqrt 3 ,0\right)$,此时直线 $l$ 的方程为\[y = - \dfrac{\sqrt 3 }{3}x + 1,\]代入椭圆方程化简得\[7{x^2} - 8\sqrt 3 x = 0,\]解得\[{x_1} = 0,{x_2} = \dfrac{8\sqrt 3 }{7},\]代入直线 $l$ 的方程得\[{y_1} = 1,{y_2} = - \dfrac{1}{7},\]所以 $D$ 点坐标为 $\left( {\dfrac{8\sqrt 3 }{7}, - \dfrac{1}{7}} \right)$,故\[|CD| = \sqrt {{{\left( {\dfrac{8\sqrt 3 }{7} - 0} \right)}^2} + {{\left( { - \dfrac{1}{7} - 1} \right)}^2}} = \dfrac{16}{7}.\]
-
当点 $P$ 异于点 $B$ 时,求证:$\overrightarrow {OP} \cdot \overrightarrow {OQ} $ 为定值.标注答案略解析当直线 $l$ 与 $x$ 轴垂直时与题意不符.
设直线 $l$ 的方程为\[y = kx + 1 \left(k \ne 0 且 k \ne \dfrac{1}{2}\right) ,\]代入椭圆方程化简得\[\left(4{k^2} + 1\right){x^2} + 8kx = 0.\]解得\[{x_1} = 0,{x_2} = \dfrac{ - 8k}{{4{k^2} + 1}},\]代入直线 $l$ 的方程得\[{y_1} = 1,{y_2} = \dfrac{{1 - 4{k^2}}}{{4{k^2} + 1}},\]所以 $D$ 点的坐标为 $\left( {\dfrac{ - 8k}{{4{k^2} + 1}},\dfrac{{1 - 4{k^2}}}{{4{k^2} + 1}}} \right)$.
又直线 $AC$ 的方程为\[\dfrac{x}{2} + y = 1,\]直线 $BD$ 的方程为\[y = \dfrac{1 + 2k}{2 - 4k}\left(x + 2\right),\]联立解得\[\begin{cases}
x = - 4k, \\
y = 2k + 1. \\
\end{cases}\]因此 $Q$ 点坐标为 $\left( - 4k,2k + 1\right)$,又 $P$ 点坐标为 $\left( { - \dfrac{1}{k},0} \right)$.所以\[\begin{split}\overrightarrow {OP} \cdot \overrightarrow {OQ} = \left( { - \dfrac{1}{k},0} \right) \cdot \left( - 4k,2k + 1\right) = 4.\end{split}\]故 $\overrightarrow {OP} \cdot \overrightarrow {OQ} $ 为定值.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2