椭圆有两顶点 $A\left( { - 1,0} \right),B\left( {1,0} \right)$,过其焦点 $F\left( {0,1} \right)$ 的直线 $l$ 与椭圆交于 $C,D$ 两点,并与 $x$ 轴交于点 $P$.直线 $AC$ 与直线 $BD$ 交于点 $Q$.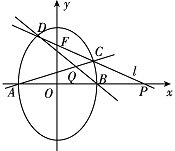

【难度】
【出处】
2011年高考四川卷(理)
【标注】
-
当 $\left| {CD} \right| = \dfrac{3}{2}\sqrt 2 $ 时,求直线 $l$ 的方程;标注答案略解析因椭圆焦点在 $y$ 轴上,设椭圆的标准方程为\[\dfrac{y^2}{a^2} + \dfrac{x^2}{b^2} = 1\left( {a > b > 0} \right),\]由已知可得\[b = 1,c = 1,\]所以\[a = \sqrt 2,\]椭圆方程为\[\dfrac{y^2}{2} + {x^2} = 1.\]直线 $l$ 垂直于 $x$ 轴时与题意不符,
设直线 $l$ 的方程为 $y = kx + 1$,将其代入椭圆方程化简得\[\left( {{k^2} + 2} \right){x^2} + 2kx - 1 = 0,\]设 $C\left( {{x_1},{y_1}} \right),D\left( {{x_2},{y_2}} \right)$,则\[\begin{split}{x_1} + {x_2} & = - \dfrac{2k}{{{k^2} + 2}}, \\ {x_1} \cdot {x_2} & = - \dfrac{1}{{{k^2} + 2}},\end{split}\]所以\[\begin{split} \left| {CD} \right| &= \sqrt {{k^2} + 1} \cdot \sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}}\\& = \dfrac{{2\sqrt 2 \left( {{k^2} + 1} \right)}}{{{k^2} + 2}}, \end{split} \]由已知得\[\dfrac{{2\sqrt 2 \left( {{k^2} + 1} \right)}}{{{k^2} + 2}} = \dfrac{3}{2}\sqrt 2 ,\]解得\[k = \pm \sqrt 2 ,\]所以直线 $l$ 的方程为\[y = \sqrt 2 x + 1 或 y = - \sqrt 2 x + 1.\] -
当点 $P$ 异于 $A,B$ 两点时,求证:$\overrightarrow {OP} \cdot \overrightarrow {OQ} $ 为定值.标注答案略解析直线 $l$ 与 $x$ 轴垂直时与题意不符,
设直线 $l$ 的方程为\[y = kx + 1\left( {k \ne 0且k \ne \pm 1} \right),\]所以 $P$ 点坐标为 $\left( { - \dfrac{1}{k},0} \right)$,设 $C\left( {{x_1},{y_1}} \right),D\left( {{x_2},{y_2}} \right)$,由(1)知\[\begin{split}{x_1} + {x_2} & = - \dfrac{2k}{{{k^2} + 2}}, \\ {x_1} \cdot {x_2} & = - \dfrac{1}{{{k^2} + 2}},\end{split}\]直线 $AC$ 的方程为\[y = \dfrac{y_1}{{{x_1} + 1}}\left( {x + 1} \right),\]直线 $BD$ 的方程为\[y = \dfrac{y_2}{{{x_2} - 1}}\left( {x - 1} \right),\]将两直线方程联立,消去 $y$ 得\[\dfrac{x + 1}{x - 1} = \dfrac{{{y_2}\left( {{x_1} + 1} \right)}}{{{y_1}\left( {{x_2} - 1} \right)}},\]因为 $ - 1 < {x_1},{x_2} < 1$,$ \therefore $ $ \dfrac{x + 1}{x - 1}$ 与 $\dfrac{y_2}{y_1}$ 异号,\[\begin{split} {\left( {\frac{x + 1}{x - 1}} \right)^2}& = \frac{{y_2^2{{\left( {{x_1} + 1} \right)}^2}}}{{y_1^2{{\left( {{x_2} - 1} \right)}^2}}} \\&= \frac{2 - 2x_2^2}{2 - 2x_1^2} \cdot \frac{{{{\left( {{x_1} + 1} \right)}^2}}}{{{{\left( {{x_2} - 1} \right)}^2}}} \\&= \frac{{\left( {1 + {x_1}} \right)\left( {1 + {x_2}} \right)}}{{\left( {1 - {x_1}} \right)\left( {1 - {x_2}} \right)}} \\&= \dfrac{{1 + \dfrac{ - 2k}{{{k^2} + 2}} + \dfrac{ - 1}{{{k^2} + 2}}}}{{1 - \dfrac{ - 2k}{{{k^2} + 2}} + \dfrac{ - 1}{{{k^2} + 2}}}}\\& = {\left( {\frac{k - 1}{k + 1}} \right)^2} ,\end{split}\]又\[\begin{split} {y_1}{y_2} &= {k^2}{x_1}{x_2} + k\left( {{x_1} + {x_2}} \right) + 1\\ &= \frac{{2\left( {1 - k} \right)\left( {1 + k} \right)}}{{{k^2} + 2}}\\ &= - \frac{{2{{\left( {1 + k} \right)}^2}}}{{{k^2} + 2}} \cdot \frac{k - 1}{k + 1},\end{split} \]$\therefore$ $ \dfrac{k - 1}{k + 1}$ 与 ${y_1}{y_2}$ 异号,$\dfrac{x + 1}{x - 1}$ 与 $\dfrac{k - 1}{k + 1}$ 同号,所以\[ \dfrac{x + 1}{x - 1} = \dfrac{k - 1}{k + 1},\]解得\[x = - k.\]因此 $Q$ 点坐标为 $\left( { - k,{y_Q}} \right) $,\[\begin{split} \overrightarrow {OP} \cdot \overrightarrow {OQ} & = \left( { - \dfrac{1}{k},0} \right) \cdot \left( { - k,{y_Q}} \right) \\& = 1,\end{split}\]故 $\overrightarrow {OP} \cdot \overrightarrow {OQ} $ 为定值.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2