设 $\lambda > 0$,点 $A$ 的坐标为 $\left( {1,1} \right)$,点 $B$ 在抛物线 $y = {x^2}$ 上运动,点 $Q$ 满足 $\overrightarrow {BQ} = \lambda \overrightarrow {QA} ,$ 经过点 $Q$ 与 $x$ 轴垂直的直线交抛物线于点 $M,$ 点 $P$ 满足 $\overrightarrow {QM} = \lambda \overrightarrow {MP} $,求点 $P$ 的轨迹方程.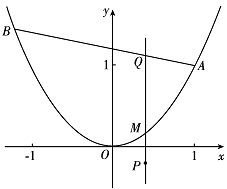

【难度】
【出处】
2011年高考安徽卷(理)
【标注】
-
标注答案略解析由 $\overrightarrow {QM} = \lambda \overrightarrow {MP} $ 知 $Q$,$M$,$P$ 三点在同一条垂直于 $x$ 轴的直线上,
故可设 $P\left(x,y\right)$,$Q\left(x,{y_0}\right)$,$M\left(x,{x^2}\right)$,则\[{x^2} - {y_0} = \lambda \left(y - {x^2}\right),\]即\[{y_0} = \left(1 + \lambda \right){x^2} - \lambda y. \quad \cdots \cdots ① \]再设 $B\left({x_1},{y_1}\right)$,由 $\overrightarrow {BQ} = \lambda \overrightarrow {QA} $,即\[\left(x - {x_1},{y_0} - {y_1}\right) = \lambda \left(1 - x,1 - {y_0}\right),\]解得\[\begin{cases}
{x_1} = \left( {1 + \lambda } \right)x - \lambda, \\
{y_1} = \left( {1 + \lambda } \right){y_0} - \lambda ,\\
\end{cases} \quad \cdots \cdots ② \]将 ① 式代入 ② 式,消去 ${y_0}$,得\[\begin{cases}{x_1} = \left(1 + \lambda \right)x - \lambda , \\
{y_1} = {\left(1 + \lambda \right)^2}{x^2} - \lambda \left(1 + \lambda \right)y - \lambda . \\
\end{cases} \quad \cdots \cdots ③ \]又点 $B$ 在抛物线 $y = {x^2}$ 上,所以\[{y_1} = x_1^2,\]再将 ③ 式代入 ${y_1} = x_1^2$,得\[\begin{split}{\left(1 + \lambda \right)^2}{x^2} - \lambda \left(1 + \lambda \right)y - \lambda & = {\left[\left(1 + \lambda \right)x - \lambda \right]^2} , \\ {\left(1 + \lambda \right)^2}{x^2} - \lambda \left(1 + \lambda \right)y - \lambda& = {\left(1 + \lambda \right)^2}{x^2} - 2\lambda \left(1 + \lambda \right)x + {\lambda ^2},\end{split} \]整理得\[2\lambda \left(1 + \lambda \right)x - \lambda \left(1 + \lambda \right)y - \lambda \left(1 + \lambda \right) = 0.\]因 $\lambda > 0$,两边同除以 $\lambda \left(1 + \lambda \right)$,得\[2x - y - 1 = 0.\]故所求点 $P$ 的轨迹方程为\[y = 2x - 1.\]
题目
问题1
答案1
解析1
备注1