已知椭圆 $C$ 的中心在原点，焦点在 $x$ 轴上，点 $F$ 是椭圆 $C$ 的右焦点，直线 $l:x=4$ 是椭圆 $C$ 的右准线，$F$ 到直线 $l$ 的距离等于 $3$．
【难度】
【出处】
无
【标注】
-
求椭圆 $C$ 的方程；标注答案$\dfrac{x^2}4+\dfrac{y^2}3=1$解析设椭圆方程为 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$，$c=\sqrt{a^2-c^2}$．根据题意有\[\begin{cases} \dfrac{a^2}{c}=4,\\
\dfrac{b^2}{c}=3,\end{cases}\]解得$$(a,b,c)=(2,\sqrt3,1),$$因此椭圆 $C$ 的方程为$$\dfrac{x^2}4+\dfrac{y^2}3=1.$$ -
点 $P$ 是椭圆 $C$ 上的动点，$PM\perp l$，垂足为 $M$，是否存在点 $P$，使得 $\triangle FPM$ 为等腰三角形？若存在，求出 $P$ 的坐标；若不存在请说明理由．标注答案存在，$P\left(\dfrac47,\pm\dfrac{3\sqrt{15}}{7}\right)$解析如图．
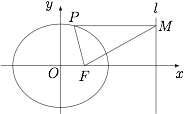根据椭圆的焦点准线定义可知 $PM=2PF$，于是若 $\triangle PFM$ 为等腰三角形，则 $PM$ 和 $MF$ 都不为底边．
若 $PF$ 为底边，则\[\cos\angle MPF=\dfrac 14,\]于是根据椭圆的焦半径公式II，有\[PF=\dfrac{b^2}{c-a\cos\angle PFO}=\dfrac{12}7,\]从而\[PM=2PF=\dfrac{24}7,\]进而 $P$ 点的横坐标为 $\dfrac 47$，代入椭圆方程可得 $P\left(\dfrac47,\pm\dfrac{3\sqrt{15}}{7}\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
