已知 $P$ 是椭圆 $E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)上一点,$F_1,F_2$ 是椭圆的左、右焦点,分别延长 $PF_1,PF_2$ 交椭圆 $E$ 于 $A,B$ 两点,直线 $AF_2$ 与直线 $AF_1$ 的公共点为 $Q$.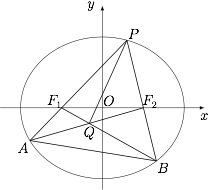

【难度】
【出处】
无
【标注】
-
求证:点 $Q$ 的轨迹是椭圆,并求其离心率 $e'$(用椭圆 $E$ 的离心率 $e$ 表示);标注答案$\dfrac{1+3e^2}{3e+e^3}$解析设椭圆 $E$ 的离心率为 $e$,$\angle PF_1F_2=\theta_1$,$\angle PF_2F_1=\theta_2$,$\angle QF_1F_2=\alpha$,$\angle QF_2F_1=\beta$,则根据椭圆离心率的三角表示,有\[e=\dfrac{\cos\dfrac{\theta_1+\theta_2}2}{\cos\dfrac{\theta_1-\theta_2}2}=\dfrac{\cos\dfrac{\pi-\theta_1+\beta}2}{\cos\dfrac{\pi-\theta_1-\beta}2}=\dfrac{\cos\dfrac{\pi-\theta_2+\alpha}2}{\cos\dfrac{\pi-\theta_2-\alpha}2},\]也即\[e=\dfrac{\cos\dfrac{\theta_1+\theta_2}2}{\cos\dfrac{\theta_1-\theta_2}2}=\dfrac{\sin\dfrac{\theta_1-\beta}2}{\sin\dfrac{\theta_1+\beta}2}=\dfrac{\sin\dfrac{\theta_2-\alpha}2}{\sin\dfrac{\theta_2+\alpha}2},\]因此\[\dfrac{1+e}{1-e}=\dfrac{\sin\dfrac{\theta_1+\beta}2+\sin\dfrac{\theta_1-\beta}2}{\sin\dfrac{\theta_1+\beta}2-\sin\dfrac{\theta_1-\beta}2}=-\dfrac{\tan\dfrac{\theta_1}2}{\tan\dfrac{\beta}2},\]类似的有\[\dfrac{1+e}{1-e}=-\dfrac{\tan\dfrac{\theta_2}2}{\tan\dfrac{\alpha}2}=-\dfrac{1}{\tan\dfrac{\theta_1}2\cdot \tan\dfrac{\theta_2}2},\]进而\[\left(\dfrac{1+e}{1-e}\right)^2=\left(-\dfrac{\tan\dfrac{\theta_2}2}{\tan\dfrac{\alpha}2}\right)\cdot \left(-\dfrac{\tan\dfrac{\theta_1}2}{\tan\dfrac{\beta}2}\right),\]有\[-\dfrac{1}{\tan\dfrac{\alpha}2\cdot \tan\dfrac{\beta}2}=\left(\dfrac{1+e}{1-e}\right)^3,\]因此 $Q$ 的轨迹是以 $F_1,F_2$ 为焦点的椭圆,且其离心率 $e'$ 满足\[\dfrac{1+e'}{1-e'}=\left(\dfrac{1+e}{1-e}\right)^3,\]解得\[e'=\dfrac{1+3e^2}{3e+e^3}.\]
-
求证:直线 $PQ$ 与直线 $AB$ 的斜率之积为定值,并求该定值(用椭圆 $E$ 的离心率 $e$ 表示).标注答案$\left(\dfrac{1-e^2}{1+e^2}\right)^2$解析设 $P(a\cos2\theta,b\sin2\theta)$,$A(a\cos2\alpha,b\sin2\alpha)$,$B(a\cos2\beta,\sin2\beta)$,$Q(am,bn)$,则根据椭圆的参数弦方程可得\[\begin{split} \tan\theta\cdot \tan\alpha&=\dfrac{e+1}{e-1},\\ \tan\theta\cdot \tan\beta&=\dfrac{e-1}{e+1},\end{split}\]且\[\begin{cases} \dfrac{n}{m-e}&=\dfrac{\sin2\alpha}{\cos2\alpha-e},\\ \dfrac{n}{m+e}&=\dfrac{\sin2\beta}{\cos2\beta+e},\end{cases}\]也即\[\begin{cases} \dfrac{n}{m-e}&=\dfrac{2\tan\alpha}{1-\tan^2\alpha-e\left(1+\tan^2\alpha\right)},\\ \dfrac{n}{m+e}&=\dfrac{2\tan\beta}{1-\tan^2\beta+e\left(1+\tan^2\beta\right)},\end{cases}\]解得\[\begin{cases} m=\dfrac{\left(e^2-1\right)\left(t^2-1\right)}{2\left(e^2+1\right)t},\\ n=\dfrac{2\left(e^2-1\right)t}{\left(e^3+3\right)\left(t^2+1\right)},\end{cases}\]其中 $t=\tan\theta$.因此直线 $PQ$ 与直线 $AB$ 的斜率之积\[\begin{split} k_{PQ}\cdot k_{AB}&=\dfrac{b\sin2\theta-bn}{a\cos2\theta-am}\cdot \left(-\dfrac ba\cdot \dfrac{1}{\tan(\alpha+\beta)}\right)\\
&=-\dfrac{b^2}{a^2}\cdot \dfrac{2t-n\left(1+t^2\right)}{1-t^2-m\left(1+t^2\right)}\cdot \dfrac{1-\left(\dfrac{e+1}{e-1}\cdot \dfrac 1t\right)\left(\dfrac{e-1}{e+1}\cdot \dfrac 1t\right)}{\dfrac{e+1}{e-1}\cdot \dfrac 1t+\dfrac{e-1}{e+1}\cdot \dfrac 1t}\\
&=-\dfrac{b^2}{a^2}\cdot \dfrac{1-e^2}{\left(1+e^2\right)^2}\\
&=\left(\dfrac{1-e^2}{1+e^2}\right)^2.\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2