题目 已知函数 $f(x)=\dfrac{4}{4x+15}$． 问题1 求方程 $f(x)-x=0$ 的实数解； 答案1 $x=-4$ 或 $x=\dfrac 14$ 解析1 题中方程即\[\dfrac{4}{4x+15}-x=0,\]解得 $x=-4$ 或 $x=\dfrac 14$． 备注1 问题2 如果数列 $\{a_n\}$ 满足 $a_1=1$，$a_{n+1}=f(a_n)$（$n\in\mathbb N^{\ast})$，是否存在实数 $c$，使得 $a_{2n}<c<a_{2n-1}$ 对所有 $n\in\mathbb N^{\ast}$ 都成立？证明你的结论； 答案2 $c=\dfrac 14$ 解析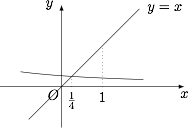2 如图．<img src="/static/images/c3c7fbd2881b3635c2effed6a89187e2.png" class="img-responsive" />利用迭代函数研究递推数列，可得\[\forall n\in \mathbb N^{\ast},a_{2n}<\dfrac 14<a_{2n-1}.\]当 $n=1$ 时，有\[a_1=1,a_2=\dfrac{4}{19},\]命题成立．而当 $x\in\left[0,1\right]$ 时，有 $f(x)\in [0,1]$，且 $f(x)$ 单调递减，因此若\[0\leqslant a_{2k}<\dfrac 14<a_{2k-1}\leqslant 1,\]则\[f(0)\geqslant f\left(a_{2k}\right)> f\left(\dfrac 14\right)> f\left(a_{2k-1}\right)\geqslant f(1),\]即\[0\leqslant \dfrac 4{19}<a_{2k}<\dfrac 14<a_{2k+1}<\dfrac{4}{15}\leqslant 1,\]进而\[f(0)\geqslant f\left(a_{2k}\right)>f\left(\dfrac 14\right)>f\left(a_{2k+1}\right)\geqslant f(1),\]因此\[a_{2k+2}<\dfrac 14<a_{2k+1},\]根据归纳原理，命题得证． 备注2 问题3 在第 $(2)$ 小题的条件下，设数列 $\{a_n\}$ 的前 $n$ 项和为 $S_n$，求证：$\dfrac 14<\dfrac{S_n}{n}\leqslant 1$． 答案3 略 解析3 欲证结论即\[0<\left(a_1-\dfrac 14\right)+\left(a_2-\dfrac 14\right)+\cdots+\left(a_n-\dfrac 14\right)\leqslant \dfrac 34n.\]根据题意，有\[a_{n+1}-\dfrac 14=\dfrac{4}{4a_n+15}-\dfrac 14=-\dfrac{a_n-\dfrac 14}{4a_n+15},\]于是\[\dfrac{a_{n+1}-\dfrac 14}{a_n-\dfrac 14}=-\dfrac{1}{4a_n+15},\]从而由第 $(2)$ 小题的结果 $a_n\in [0,1],n\in\mathbb N^{\ast}$，于是\[-\dfrac{1}{15}\leqslant \dfrac{a_{n+1}-\dfrac 14}{a_n-\dfrac 14}\leqslant -\dfrac{1}{19},\]因此当 $n\geqslant 2$ 时，有\[0<\left(a_1-\dfrac 14\right)+\left(a_2-\dfrac 14\right)+\cdots+\left(a_n-\dfrac 14\right)\leqslant \dfrac{a_1-\dfrac 14}{1-\dfrac{1}{15}}=\dfrac{45}{56},\]而当 $n=1$ 时命题显然成立．因此原命题得证． 备注3