设函数 $f\left(x\right)=\left(x-1\right)\cdot|x-a|\left(a\in \mathbb R\right)$．
【难度】
【出处】
无
【标注】
-
当 $a=2$ 且 $x\geqslant0$，关于 $x$ 的方程 $f\left(x\right)=kx-\dfrac29$ 有三个实数解 $x_1,x_2,x_3$，若 $t=\max\limits \left\{x_1,x_2,x_3\right\}$，求实数 $t$ 的取值范围；标注答案$\left(2,\dfrac{5+\sqrt 5}3\right)$解析根据题意，当 $a=2$ 且 $x\geqslant0$ 时，有\[ f\left(x\right)= \begin{cases}\left(x-1\right)\left(x-2\right) ,&x\geqslant2\\-\left(x-1\right)\left(x-2\right),&0\leqslant x<2\end{cases} ,\]其图象为：
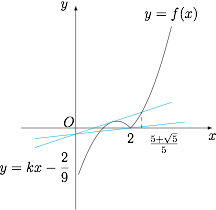若关于 $x$ 的方程 $f\left(x\right)=kx-\dfrac29$ 有三个实数解 $x_1,x_2,x_3$，则直线 $y=kx-\dfrac29 $ 位于图中两条直线之间，进而可得实数 $k$ 的取值范围是 $\left(\dfrac 19,\dfrac 13\right)$，此时最大实数解 $t$ 的取值范围是 $\left(2,\dfrac{5+\sqrt 5}3\right)$． -
当 $a\in\left(-1,\dfrac15\right)$ 时，若关于 $x$ 的方程 $f\left(x\right)=2x-\dfrac12a$ 有三个实数解 $x_1,x_2,x_3$，求 $x_1+x_2+x_3$ 的取值范围．标注答案$\left(\dfrac{2-\sqrt{6}}{2},\dfrac{8+\sqrt{226}}{10}\right)$解析设函数\[h\left(x\right)=\left(x-1\right)\cdot |x-a|-2x+\dfrac 12a,\]也即\[h(x)= \begin{cases}
x^2-\left(a+3\right)x+\dfrac 32a,&x\geqslant a,\\
-x^2+\left(a-1\right)x-\dfrac 12a,&x<a,
\end{cases} \]因为 $-1<a<\dfrac 15$，所以 $\dfrac{a-1}2<a<\dfrac{a+3}2$，且注意到 $h\left(a\right)=-\dfrac 32a$．情形一 当 $0<a<\dfrac 15$ 时，因为\[\begin{cases}
\left(a-1\right)^2-4\cdot \dfrac 12a>0,\\
h\left(a\right)=-\dfrac 32a<0,
\end{cases} \]所以\[\begin{split}t&=x_1+x_2+x_3\\&=\left(a-1\right)+\dfrac{a+3+\sqrt{a^2+9}}2\\&=\dfrac 12\left(3a+1+\sqrt{a^2+9}\right).\end{split}\]于是 $x_1+x_2+x_3$ 的取值范围是 $ \left(2,\dfrac{8+\sqrt{226}}{10}\right)$．情形二 当 $-1<a\leqslant 0$ 时，因为\[\begin{cases}
\left(a+3\right)^2-4\cdot \dfrac 32a>0,\\
h\left(a\right)=-\dfrac 32a\geqslant 0,
\end{cases} \]所以\[\begin{split}t&=x_1+x_2+x_3\\&=\left(a+3\right)+\dfrac{a-1-\sqrt{a^2-4a+1}}2\\&=\dfrac 12\left(3a+5-\sqrt{\left(a-2\right)^2-3}\right)\end{split}\]于是 $x_1+x_2+x_3$ 的取值范围是 $\left(\dfrac{2-\sqrt{6}}{2},2\right]$．
综上所述，$x_1+x_2+x_3$ 的取值范围是 $\left(\dfrac{2-\sqrt{6}}{2},\dfrac{8+\sqrt{226}}{10}\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
