题目 已知函数 $f(x)=(x-t)|x|$（$t \in \mathbb R$）． 问题1 根据 $t$ 的不同取值，试判断 $f(x)$ 的奇偶性并说明理由； 答案1 当 $t=0$ 时，函数 $f(x)$ 为奇函数；当 $t\neq 0$ 时，函数 $f(x)$ 为非奇非偶函数 解析1 函数 $f(x)$ 的定义域为 $\mathbb R$，关于原点对称，又$$f(x)=\begin{cases} x(x-t), & x \geqslant 0,\\ -x(x-t),& x<0.\end{cases}$$而$$f(-x)=\begin{cases} -x(x+t), & x \geqslant 0,\\ x(x+t),& x<0.\end{cases}$$当 $t=0$ 时，$$f(-x)=-f(x),$$此时函数 $f(x)$ 为奇函数；<br/>当 $t\neq 0$ 时，$$f(-x)\neq -f(x) \land f(-x)\neq f(x) ,$$此时函数 $f(x)$ 为非奇非偶函数． 备注1 问题2 试讨论函数 $f(x)$ 的单调区间； 答案2 当 $t=0$ 时，函数 $f(x)$ 的单调递增区间是 $\mathbb R$；<br/>当 $t>0$ 时，函数 $f(x)$ 的单调递增区间是 $(-\infty,0)$ 和 $\left(\dfrac t2,+\infty\right)$，单调递减区间为 $\left(0,\dfrac t2\right)$；<br/>当 $t<0$ 时，函数 $f(x)$ 的单调递增区间是 $\left(-\infty,\dfrac t2\right)$ 和 $(0,+\infty)$，单调递减区间为 $\left(\dfrac t2,0\right)$ 解析2 注意到分段函数 $f(x)$ 是由开口方向相反的两个二次函数组成的，而这两个二次函数图象恒过定点 $(0,0)$ 且共对称轴 $x=\dfrac t2$，函数 $f(x)$ 各种情况下的图象如图所示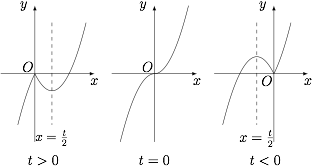：<img src="/static/images/238d59c20dd9b9f8d3b164f5f67ffd3d.png" class="img-responsive" />故当 $t=0$ 时，函数 $f(x)$ 的单调递增区间是 $\mathbb R$；<br/>当 $t>0$ 时，函数 $f(x)$ 的单调递增区间是 $(-\infty,0)$ 和 $\left(\dfrac t2,+\infty\right)$，单调递减区间为 $\left(0,\dfrac t2\right)$；<br/>当 $t<0$ 时，函数 $f(x)$ 的单调递增区间是 $\left(-\infty,\dfrac t2\right)$ 和 $(0,+\infty)$，单调递减区间为 $\left(\dfrac t2,0\right)$ 备注2 问题3 当 $t>0$ 时，若 $f(x)$ 在区间 $[-1,2]$ 上的最大值为 $M(t)$，最小值为 $m(t)$，求 $M(t)\cdot m(t)$ 的最小值． 答案3 略 解析3 由第 $(2)$ 小题中函数 $f(x)$ 的单调性知，$f(x)$ 在区间 $[-1,2]$ 上的最大值为$$\max \{f(0),f(2)\}.$$又 $f(-1)=-1-t$，$f\left(\dfrac t2 \right)=-\dfrac {t^2}{4}$，$f(2)=4-2t$，$f(0)=0$．<br/><case>情形一</case>当 $\dfrac t2 \geqslant 1$，即 $t \geqslant 2$ 时，最大值为$$M(t)=f(0)=0,$$此时$$M(t)\cdot m(t)=0.$$<case>情形二</case>当 $0<\dfrac t2 < 1$，即 $0<t <2$ 时，最大值为$$M(t)=f(2)=4-2t,$$最小值为$$f(-1)=-1-t.$$此时$$M(t)\cdot m(t)= (4-2t)(-1-t) =2\left(t-\dfrac 12\right)^2-\dfrac 92.$$故当 $t=\dfrac 12$ 时，$M(t)\cdot m(t)$ 取得最小值为 $-\dfrac 92$． 备注3