如图所示，正四面体 $ABCD$ 的棱长是 $1$，$P$ 是 $\triangle BCD$ 的中心，$M,N$ 分别在面 $ABD,ACD$ 上运动，求 $\triangle PMN$ 的周长的最小值．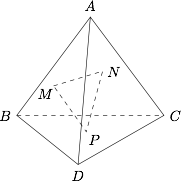
【难度】
【出处】
2010年第二十一届“希望杯”全国数学邀请赛高二（二试）
【标注】
【答案】
$\dfrac89$
【解析】
取点 $P$ 关于面 $ABD$ 的对称点，记为 $P'$；关于面 $ACD$ 的对称点，记为 $P''$，如图．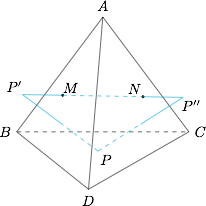
因此，有$$PM+PN+MN\geqslant P'P'',$$所以 $P'P''$ 即为 $\triangle PMN$ 的周长最小值．
设点 $C$ 到平面 $ABD$ 的距离为 $d$，则有$$PP'=PP''=d=\dfrac{2\sqrt6}{9},$$设二面角 $B-AD-C$ 的平面角为 $\theta$，可计算得$$\cos\theta=\dfrac13,$$由题可知 $\angle P'PP''+\theta=\pi$，则有$$\left|\overrightarrow{P'P''}\right|=\left|\overrightarrow{PP''}-\overrightarrow{PP'}\right|=\sqrt{\left|\overrightarrow{PP'}\right|^2+\left|\overrightarrow{PP''}\right|^2+2\cdot\left|\overrightarrow{PP'}\right|\cdot\left|\overrightarrow{PP''}\right|\cdot\cos\angle P'PP''}=\dfrac89,$$因此 $\triangle PMN$ 的周长的最小值为 $\dfrac89$．
因此，有$$PM+PN+MN\geqslant P'P'',$$所以 $P'P''$ 即为 $\triangle PMN$ 的周长最小值．设点 $C$ 到平面 $ABD$ 的距离为 $d$，则有$$PP'=PP''=d=\dfrac{2\sqrt6}{9},$$设二面角 $B-AD-C$ 的平面角为 $\theta$，可计算得$$\cos\theta=\dfrac13,$$由题可知 $\angle P'PP''+\theta=\pi$，则有$$\left|\overrightarrow{P'P''}\right|=\left|\overrightarrow{PP''}-\overrightarrow{PP'}\right|=\sqrt{\left|\overrightarrow{PP'}\right|^2+\left|\overrightarrow{PP''}\right|^2+2\cdot\left|\overrightarrow{PP'}\right|\cdot\left|\overrightarrow{PP''}\right|\cdot\cos\angle P'PP''}=\dfrac89,$$因此 $\triangle PMN$ 的周长的最小值为 $\dfrac89$．
答案
解析
备注
