如图，在圆锥 $PO$ 中，已知 $PO = \sqrt 2 $，$ \odot O$ 的直径 $AB = 2$，点 $C$ 在 $\overparen {AB}$ 上，且 $\angle CAB = 30^\circ$，$D$ 为 $AC$ 的中点．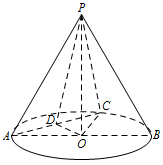
【难度】
【出处】
2011年高考湖南卷（文）
【标注】
-
证明：$AC \perp $ 平面 $POD$；标注答案略解析因为 $OA = OC$，$D$ 是 $AC$ 的中点，所以 $AC \perp OD$．
又 $PO \perp $ 底面 $ \odot O$，$AC \subset $ 底面 $ \odot O$，所以 $AC \perp PO$．
$OD$，$PO$ 是平面 $POD$ 内的两条相交直线，
所以 $AC \perp $ 平面 $POD$． -
求直线 $OC$ 和平面 $PAC$ 所成角的正弦值．标注答案略解析由（1）知，$AC \perp $ 平面 $POD$，又 $AC \subset $ 平面 $PAC$，所以平面 $POD \perp $ 平面 $PAC$，
如图，在平面 $POD$ 中，过 $O$ 作 $OH \perp PD$ 于 $H$．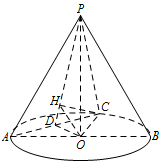
则 $OH \perp $ 平面 $PAC$．
连接 $CH$，则 $CH$ 是 $OC$ 在平面 $PAC$ 上的射影，
所以 $\angle OCH$ 是直线 $OC$ 和平面 $PAC$ 所成的角．
在 ${\mathrm{Rt}}\triangle POD$ 中，\[\begin{split}OH & = \dfrac{PO \cdot OD}{{\sqrt {{PO^2} + {OD^2}} }} \\& = \dfrac{{\sqrt 2 \times \dfrac{1}{2}}}{{\sqrt {2 + \dfrac{1}{4}} }} \\& = \dfrac{\sqrt 2 }{3},\end{split}\]在 ${\mathrm{Rt}}\triangle OHC$ 中，\[\sin \angle OCH = \dfrac{OH}{OC} = \dfrac{\sqrt 2 }{3}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
