如图,长方体物体 $E$ 在雨中沿面 $P$(面积为 $S$)的垂直方向作匀速移动,速度为 $v\left( {v > 0} \right)$,雨速沿 $E$ 移动方向的分速度为 $c\left( {c \in {\mathbb {R}}} \right)$.$E$ 移动时单位时间内的淋雨量包括两部分:(1)$P$ 或 $P$ 的平行面(只有一个面淋雨)的淋雨量,假设其值与 $\left| {v - c} \right| \times S$ 成正比,比例系数为 $\dfrac{1}{10}$;(2)其他面的淋雨量之和,其值为 $\dfrac{1}{2}$,记 $y$ 为 $E$ 移动过程中的总淋雨量,当移动距离 $d = 100$,面积 $S = \dfrac{3}{2}$ 时.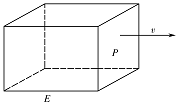

【难度】
【出处】
2011年高考湖南卷(理)
【标注】
-
写出 $y$ 的表达式;标注答案$ y = \dfrac{5}{v}\left( {3|v - c| + 10} \right) $解析由题意知,$E$ 移动时单位时间内的淋雨量为\[\dfrac{3}{20}|v - c| + \dfrac{1}{2},\]故\[ \begin{split}y & = \dfrac{100}{v}\left( {\dfrac{3}{20}|v - c| + \dfrac{1}{2}} \right) \\& = \dfrac{5}{v}\left( {3|v - c| + 10} \right).\end{split} \]
-
设 $0 < v \leqslant 10,0 < c \leqslant 5,$ 试根据 $c$ 的不同取值范围,确定移动速度 $v$,使总淋雨量 $y$ 最少.标注答案当 $0 < c \leqslant \dfrac{10}{3}$ 时,${y_{\min }} = 20 - \dfrac{3c}{2}$;
当 $\dfrac{10}{3} < c \leqslant 5$ 时,${y_{\min }} = \dfrac{50}{c}$解析由(1)知,当 $0 < v \leqslant c$ 时,\[ \begin{split}y & = \dfrac{5}{v}\left( {3c - 3v + 10} \right) \\& = \dfrac{{5\left( {3c + 10} \right)}}{v} - 15;\end{split} \]当 $c < v \leqslant 10$ 时,\[ \begin{split}y & = \dfrac{5}{v}\left( {3v - 3c + 10} \right) \\& = \dfrac{{5\left( {10 - 3c} \right)}}{v} + 15.\end{split} \]故\[y = { \begin{cases}\dfrac{{5\left( {3c + 10} \right)}}{v} - 15,&0 < v \leqslant c, \\
\dfrac{{5\left( {10 - 3c} \right)}}{v} + 15,&c < v \leqslant 10. \\
\end{cases} }\]① 当 $0 < c \leqslant \dfrac{10}{3}$ 时,$y$ 是关于 $v$ 的减函数.故当 $v = 10$ 时,\[{y_{\min }} = 20 - \dfrac{3c}{2}.\]② 当 $\dfrac{10}{3} < c \leqslant 5$ 时,
在 $\left(0,c\right]$ 上,$y$ 是关于 $v$ 的减函数;
在 $\left(c,10\right]$ 上,$y$ 是关于 $v$ 的增函数;
故当 $v = c$ 时,\[{y_{\min }} = \dfrac{50}{c}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2