如图,椭圆 ${C_1}:\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\left( {a > b > 0} \right)$ 的离心率为 $\dfrac{\sqrt 3 }{2}$,$x$ 轴被曲线 ${C_2}:y = {x^2} - b$ 截得的线段长等于 ${C_1}$ 的长半轴长.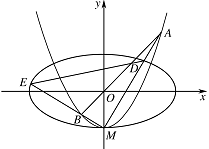

【难度】
【出处】
2011年高考湖南卷(理)
【标注】
-
求 ${C_1},{C_2}$ 的方程;标注答案略解析由题意知\[e = \dfrac{c}{a} = \dfrac{\sqrt 3 }{2},\]从而\[a = 2b,\]又 $2\sqrt b = a$,解得\[a = 2,b = 1.\]故 ${C_1},{C_2}$ 的方程分别为 $\dfrac{x^2}{4} + {y^2} = 1$,$y = {x^2} - 1$.
-
设 ${C_2}$ 与 $y$ 轴的交点为 $M$,过坐标原点 $O$ 的直线 $l$ 与 ${C_2}$ 相交于点 $A,B$,直线 $MA,MB$ 分别与 ${C_1}$ 相交与点 $D,E$.
① 证明:$MD \perp ME$;
② 记 $\triangle MAB,\triangle MDE$ 的面积分别是 ${S_1},{S_2}$.问:是否存在直线 $l$,使得 $\dfrac{S_1}{S_2} = \dfrac{17}{32}$?请说明理由.标注答案略解析① 由题意知,直线 $l$ 的斜率存在,设为 $k$,则直线 $l$ 的方程为 $y = kx$.
由\[{\begin{cases}
y = kx ,\\
y = {x^2} - 1 .\\
\end{cases}}\]得\[{x^2} - kx - 1 = 0,\]设 $A\left( {{x_1},{y_1}} \right),B\left( {{x_2},{y_2}} \right)$,则 ${x_1},{x_2}$ 是上述方程的两个实根,于是\[{x_1} + {x_2} = k,{x_1}{x_2} = - 1.\]又点 $M$ 的坐标为 $\left( {0, - 1} \right)$,所以\[\begin{split}{k_{MA}} \cdot {k_{MB}} & = \dfrac{{{y_1} + 1}}{x_1} \cdot \dfrac{{{y_2} + 1}}{x_2} = \dfrac{{\left( {k{x_1} + 1} \right)\left( {k{x_2} + 1} \right)}}{{{x_1}{x_2}}} \\& = \dfrac{{{k^2}{x_1}{x_2} + k\left( {{x_1} + {x_2}} \right) + 1}}{{{x_1}{x_2}}} = \dfrac{{ - {k^2} + {k^2} + 1}}{ - 1} = - 1,\end{split}\]故 $MA \perp MB$,即 $MD \perp ME$.
② 设直线 $MA$ 的斜率为 ${k_1}$,则直线 $MA$ 的方程为 $y = {k_1}x - 1$,由\[{\begin{cases}
y = {k_1}x - 1 ,\\
y = {x^2} - 1. \\
\end{cases}}\]解得\[{\begin{cases}x = 0 ,\\
y = - 1 .\\
\end{cases}} 或 {\begin{cases}x = {k_1}, \\
y = k_1^2 - 1. \\
\end{cases}}\]则点 $A$ 的坐标为 $\left( {{k_1},{k_1^2} - 1} \right)$.
又直线 $MB$ 的斜率为 $ - \dfrac{1}{k_1}$,同理可得点 $B$ 的坐标为 $\left( { - \dfrac{1}{k_1},\dfrac{1}{k_1^2} - 1} \right)$.
于是\[ {S_1} = \dfrac{1}{2}|MA| \cdot |MB| = \dfrac{1}{2}\sqrt {1 + {k_1^2}} \cdot |{k_1}| \cdot \sqrt {1 + \dfrac{1}{k_1^2}} \cdot \left| { - \dfrac{1}{k_1}} \right| = \dfrac{{1 + {k_1^2}}}{{2|{k_1}|}}. \]由\[{\begin{cases}
y = {k_1}x - 1, \\
{x^2} + 4{y^2} - 4 = 0. \\
\end{cases}}\]得\[\left( {1 + 4{k_1^2}} \right){x^2} - 8{k_1}x = 0,\]解得\[{\begin{cases}x = 0 ,\\
y = - 1 .\\
\end{cases}} 或 {\begin{cases}x = \dfrac{{8{k_1}}}{{1 + 4{k_1^2}}}, \\
y = \dfrac{{4{k_1^2} - 1}}{{1 + 4{k_1^2}}} .\\
\end{cases}}\]则点 $D$ 的坐标为 $\left( {\dfrac{{8{k_1}}}{{1 + 4{k_1^2}}},\dfrac{{4{k_1^2} - 1}}{{1 + 4{k_1^2}}}} \right)$.
又直线 $ME$ 的斜率为 $ - \dfrac{1}{k_1}$,同理可得点 $E$ 的坐标为 $\left( {\dfrac{{ - 8{k_1}}}{{4 + {k_1^2}}},\dfrac{{4 - {k_1^2}}}{{4 + {k_1^2}}}} \right)$.
于是\[ {S_2} = \dfrac{1}{2}|MD| \cdot |ME| = \dfrac{{32\left( {1 + {k_1^2}} \right) \cdot |{k_1}|}}{{\left( {1 + 4{k_1^2}} \right)\left( {4 + {k_1^2}} \right)}}, \]因此\[\dfrac{S_1}{S_2} = \dfrac{1}{64}\left( {4{k_1^2} + \dfrac{4}{k_1^2} + 17} \right).\]由题意知\[\dfrac{1}{64}\left( {4{k_1^2} + \dfrac{4}{k_1^2} + 17} \right) = \dfrac{17}{32},\]解得\[{k_1^2} = 4 或 {k_1^2} = \dfrac{1}{4}.\]又由点 $A,B$ 的坐标可知\[k = \dfrac{{{k_1^2} - \dfrac{1}{k_1^2}}}{{{k_1} + \dfrac{1}{k_1}}} = {k_1} - \dfrac{1}{k_1},\]所以 $k = \pm \dfrac{3}{2}$.
故满足条件的直线 $l$ 存在,且有两条,其方程分别为 $y = \dfrac{3}{2}x $ 和 $ y = - \dfrac{3}{2}x$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2