题目 用 $[a]$ 表示不大于 $a$ 的最大整数．令集合 $P=\{1,2,3,4,5\}$，对任意 $k\in P$ 和 $m\in \mathbb N^+$，定义 $\displaystyle f(m,k)=\sum\limits_{i=1}^{5}\left[m\sqrt{\dfrac{k+1}{i+1}}\right]$，集合 $A=\{m\sqrt{k+1}\mid m\in {\mathbb N^+},k\in P\}$，并将集合 $A$ 中的元素按照从小到大的顺序排列，记为数列 $\{a_n\}$． 问题1 求 $f(1,2)$ 的值； 答案1 $2$ 解析1 由已知$$\begin{split}f(1,2)&=\left[\sqrt{\dfrac 32}\right]+\left[\sqrt{\dfrac 33}\right]+\left[\sqrt{\dfrac 34}\right]+\left[\sqrt{\dfrac 35}\right]+\left[\sqrt{\dfrac 36}\right]\\ &=1+1+0+0+0=2.\end{split}$$ 备注1 问题2 求 $a_9$ 的值； 答案2 $3\sqrt 2$ 解析2 数列 $\{a_n\}$ 是将集合 $A=\{m\sqrt{k+1}|m\in {\mathbb N^+},k\in P\}$ 中的元素按从小到大的顺序排成而成，如下表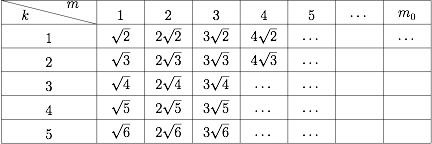．<img src="/static/images/e212a31d81a2a915a41ee967ec962da9.png" class="img-responsive" />从上表可知，每一行从左到右数字逐渐增大，每一列从上到下数字逐渐增大．<br/>且$$\sqrt 2<\sqrt 3<\sqrt 4<\sqrt 5<\sqrt 6<2\sqrt 2<2\sqrt 3<2\sqrt 4<3\sqrt 2<2\sqrt 5<\cdots ,$$所以 $a_9=3\sqrt 2$． 备注2 问题3 求证：在数列 $\{a_n\}$ 中，不大于 $m_0\sqrt{k_0+1}$ 的项共有 $f(m_0,k_0)$ 项． 答案3 略 解析3 任取 $m_1,m_2\in {\mathbb N^+}$，$k_1,k_2\in P$，<br/>若$$m_1\sqrt{k_1+1}=m_2\sqrt{k_2+1},$$则必有$$m_1=m_2,k_1=k_2,$$即在⑵表格中不会有两项的值相等．<br/>对于 $m_0\sqrt{k_0+1}$ 而言，若在⑵表格中的第一行共有 $m_1$ 的数不大于 $m_0\sqrt{k_0+1}$，<br/>则$$m_1\sqrt 2 \leqslant m_2\sqrt{k_0+1},$$即$$m_1\leqslant \dfrac{m_0\sqrt{k_0+1}}{\sqrt 2},$$所以$$m_1=\left[\dfrac{m_0\sqrt{k_0+1}}{\sqrt 2}\right].$$同理，第二行共有 $m_2$ 的数不大于 $m_0\sqrt{k_0+1}$，有$$m_2=\left[\dfrac{m_0\sqrt{k_0+1}}{\sqrt 3}\right],$$第 $i$ 行共有 $m_i$ 的数不大于 $m_0\sqrt{k_0+1}$，有$$m_i=\left[\dfrac{m_0\sqrt{k_0+1}}{\sqrt{i+1}}\right],$$所以，在数列 $\{a_n\}$ 中，不大于 $m_0\sqrt{k_0+1}$ 的项共有 $\displaystyle \sum\limits_{i=1}^5\left[m_0\sqrt{\dfrac{k_0+1}{i+1}}\right]$ 项，即 $f(m_0,k_0)$ 项． 备注3