已知异面直线 $AB,CD$，求证：以 $AB$ 为轴将 $CD$ 旋转一周得到的曲面是双曲面（双曲面即双曲线绕其对称轴旋转生成的曲面，分单叶双曲面与双叶双曲面）．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
如图，设 $OH$ 是异面直线 $AB,CD$ 的公垂线段，并建立平面直角坐标系 $xOy$．$P$ 点为 $D$ 点在旋转一周的过程中在轴截面 $xOy$ 上的对应点．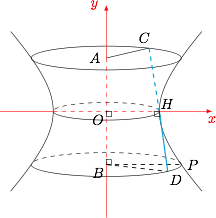
设 $\overrightarrow{AB}$ 和 $\overrightarrow{CD}$ 的夹角为 $\theta$．由\[\overrightarrow{BD}=\overrightarrow{BO}+\overrightarrow{OH}+\overrightarrow{HD},\]可得\[BD^2=BO^2+OH^2+HD^2-2\cdot BO\cdot HD\cdot\cos\theta,\]又 $BO=HD\cdot\cos\theta$，且 $BD=BP$，于是\[BP^2-\left(\dfrac{1}{\cos^2\theta}-1\right)BO^2=OH^2,\]也即\[BP^2-\tan^2\theta\cdot BO^2=OH^2,\]此数量关系符合双曲线方程，因此命题得证．
设 $\overrightarrow{AB}$ 和 $\overrightarrow{CD}$ 的夹角为 $\theta$．由\[\overrightarrow{BD}=\overrightarrow{BO}+\overrightarrow{OH}+\overrightarrow{HD},\]可得\[BD^2=BO^2+OH^2+HD^2-2\cdot BO\cdot HD\cdot\cos\theta,\]又 $BO=HD\cdot\cos\theta$，且 $BD=BP$，于是\[BP^2-\left(\dfrac{1}{\cos^2\theta}-1\right)BO^2=OH^2,\]也即\[BP^2-\tan^2\theta\cdot BO^2=OH^2,\]此数量关系符合双曲线方程，因此命题得证．
答案
解析
备注
