给定两个相交的圆 $O_1$ 和 $O_2$.记 $A,B$ 为两圆的交点.一条动直线经过 $B$ 点与圆 $O_1$ 相交于另一点 $C$,与圆 $O_2$ 相交于另一点 $D$,且点 $B$ 在线段 $CD$ 内部,过 $C$ 的圆 $O_1$ 的切线与过 $D$ 的圆 $O_2$ 的切线相交于 $M$,连接 $AM$ 交 $CD$ 于 $E$,过 $E$ 作 $DM$ 的平行线交 $AD$ 于 $K$,求证:直线 $BK$ 是圆 $O_1$ 的切线.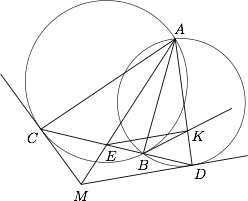

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
根据题意,有\[\angle BDM=\angle BAD=\angle BEK,\]于是 $A,E,B,K$ 四点共圆,进而\[\angle ABK=\angle AEK=\angle AMD.\]又由于 $\angle MCD=\angle CAB,\angle MDC=\angle BAD,$ 于是\[\angle CMD+\angle MCD+\angle MDC=\angle CMD+\angle CAB+\angle BAD=\angle CMD+\angle CAD=180^\circ,\]因此 $A,C,M,D$ 四点共圆,进而\[\angle ACD=\angle AMD.\]综上所述,有\[\angle ABK=\angle ACD,\]由弦切角定理的逆定理,$BK$ 是圆 $O_1$ 的切线.
答案
解析
备注