如图,椭圆的中心为原点 $O$,离心率 $e = \dfrac{{\sqrt 2 }}{2}$,一条准线的方程为 $x = 2\sqrt 2 $.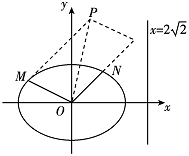

【难度】
【出处】
2011年高考重庆卷(理)
【标注】
-
求该椭圆的标准方程;标注答案略解析由\[e = \dfrac{c}{a} = \dfrac{{\sqrt 2 }}{2} , \dfrac{{{a^2}}}{c} = 2\sqrt 2 ,\]解得\[a = 2,c = \sqrt 2 ,{b^2} = {a^2} - {c^2} = 2,\]故椭圆的标准方程为\[\dfrac{{{x^2}}}{4} + \dfrac{{{y^2}}}{2} = 1.\]
-
设动点 $P$ 满足:$\overrightarrow {OP} = \overrightarrow {OM} + 2\overrightarrow {ON} $,其中 $M$,$N$ 是椭圆上的点,直线 $OM$ 与 $ON$ 的斜率之积为 $ - \dfrac{1}{2}$.问:是否存在两个定点 ${F_1}$,${F_2}$,使得 $\left| {P{F_1}} \right| + \left| {P{F_2}} \right|$ 为定值?若存在,求 ${F_1}$,${F_2}$ 的坐标;若不存在,说明理由.标注答案略解析设 $P\left( {x,y} \right)$,$M\left( {{x_1},{y_1}} \right)$,$N\left( {{x_2},{y_2}} \right)$,则由 $\overrightarrow {OP} = \overrightarrow {OM} + 2\overrightarrow {ON} $ 得\[\begin{split}\left( {x,y} \right) = \left( {{x_1},{y_1}} \right) + 2\left( {{x_2},{y_2}} \right) = \left( {{x_1} + 2{x_2},{y_1} + 2{y_2}} \right),\end{split}\]即\[\begin{split}x & = {x_1} + 2{x_2} ,\\ y & = {y_1} + 2{y_2}.\end{split}\]因为点 $M$,$N$ 在椭圆 ${x^2} + 2{y^2} = 4$ 上,所以\[\begin{split}x_1^2 + 2y_1^2 &= 4 , \\ x_2^2 + 2y_2^2 & = 4,\end{split}\]故\[\begin{split}{x^2} + 2{y^2} & = \left( {x_1^2 + 4x_2^2 + 4{x_1}{x_2}} \right) + 2\left( {y_1^2 + 4y_2^2 + 4{y_1}{y_2}} \right) \\& = \left( {x_1^2 + 2y_1^2} \right) + 4\left( {x_2^2 + 2y_2^2} \right) + 4\left( {{x_1}{x_2} + 2{y_1}{y_2}} \right) \\&
= 20 + 4\left( {{x_1}{x_2} + 2{y_1}{y_2}} \right).\end{split}\]设 ${k_{OM}}$,${k_{ON}}$ 分别为直线 $OM$,$ON $ 的斜率,由题设条件知\[{k_{OM}} \cdot {k_{ON}} = \dfrac{{{y_1}{y_2}}}{{{x_1}{x_2}}} = - \dfrac{1}{2},\]因此\[{x_1}{x_2} + 2{y_1}{y_2} = 0,\]所以\[{x^2} + 2{y^2} = 20.\]所以 $P$ 点是椭圆 $\dfrac{{{x^2}}}{{{{\left( {2\sqrt 5 } \right)}^2}}} + \dfrac{{{y^2}}}{{{{\left( {\sqrt {10} } \right)}^2}}} = 1$ 上的点.
设该椭圆的左、右焦点为 ${F_1}$,${F_2}$,则由椭圆的定义 ${\left|{P{F_1}}\right|} + {\left|{P{F_2}}\right|}$ 为定值,又因为\[c = \sqrt{\left(2\sqrt 5\right)^2 - \left(\sqrt{10}\right)^2} = \sqrt{10},\]因此两焦点的坐标为\[{F_1}\left( {-\sqrt {10} ,0} \right),{F_2}\left( {\sqrt {10} ,0} \right).\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2