如图,在四面体 $ABCD$ 中,平面 $ABC \perp 平面 ACD$,$AB \perp BC$,$AD = CD$,$\angle CAD = 30^\circ $.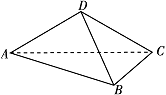

【难度】
【出处】
2011年高考重庆卷(理)
【标注】
-
若 $AD = 2$,$AB = 2BC$,求四面体 $ABCD$ 的体积;标注答案$\dfrac45$解析如图,设 $F$ 为 $AC$ 的中点.
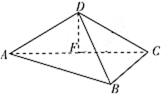 由于 $AD = CD$,所以 $DF \perp AC$,故由平面 $ABC \perp 平面 ACD$,
由于 $AD = CD$,所以 $DF \perp AC$,故由平面 $ABC \perp 平面 ACD$,
知 $DF \perp 平面 ABC$,即 $DF$ 是四面体 $ABCD$ 的面 $ABC$ 上的高,且\[DF = AD\sin 30^\circ = 1 , AF = AD\cos 30^\circ = \sqrt 3.\]在 ${\mathrm {Rt}} \triangle ABC$ 中,因 $AC = 2AF = 2\sqrt 3$,$ AB= 2BC$.由勾股定理易知\[BC = \dfrac{{2\sqrt {15} }}{5} , AB = \dfrac{{4\sqrt {15} }}{5}.\]故四面体 $ABCD$ 的体积\[ \begin{split}V & = \dfrac{1}{3} \cdot {S_{\triangle ABC}} \cdot DF \\& = \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{{4\sqrt {15} }}{5} \times \dfrac{{2\sqrt {15} }}{5} \\& = \dfrac{4}{5}.\end{split} \] -
若二面角 $C - AB - D$ 为 $60^\circ $,求异面直线 $AD$ 与 $BC$ 所成角的余弦值.标注答案$\dfrac{\sqrt 3 }{6}$解析解法一:
如图,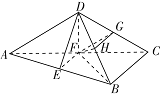 设 $G$,$H$ 分别为边 $CD$,$BD$ 的中点,连接 $ FG $,$ GH$.则 $FG\parallel AD$,$GH\parallel BC$.
设 $G$,$H$ 分别为边 $CD$,$BD$ 的中点,连接 $ FG $,$ GH$.则 $FG\parallel AD$,$GH\parallel BC$.
从而 $\angle FGH$ 是异面直线 $AD$ 与 $BC$ 所成的角或其补角.
设 $E$ 为边 $AB$ 的中点,连接 $ DE $,$ EF$,$BF $.则 $EF\parallel BC$,由 $AB \perp BC$,知 $EF \perp AB$,
由(1)有 $DF \perp 平面 ABC$,故知 $DE \perp AB$.
所以 $\angle DEF$ 为二面角 $C - AB - D$ 的平面角.
由题设知 $\angle DEF = 60^\circ$.设 $AD = a$,则\[DF = AD \cdot \sin \angle CAD = \dfrac{a}{2}.\]在 ${\mathrm {Rt}} \triangle DEF$ 中,\[EF = DF \cdot \cot \angle DEF = \dfrac{a}{2} \cdot \dfrac{\sqrt 3 }{3} = \dfrac{\sqrt 3 }{6}a,\]从而\[GH = \dfrac{1}{2}BC = EF = \dfrac{\sqrt 3 }{6}a.\]因 ${\mathrm {Rt}} \triangle ADE \cong {\mathrm {Rt}} \triangle BDE$,故\[BD = AD = a,\]从而,在 ${\mathrm {Rt}} \triangle BDF$ 中,$FH = \dfrac{1}{2}BD = \dfrac{a}{2}$,又 $FG = \dfrac{1}{2}AD = \dfrac{a}{2}$,
从而在 $\triangle FGH$ 中,因 $FG = FH$,由余弦定理得\[ \begin{split}\cos \angle FGH & = \dfrac{{F{G^2} + G{H^2} - F{H^2}}}{2FG \cdot GH} \\& = \dfrac{GH}{2FG} = \dfrac{\sqrt 3 }{6}.\end{split} \]因此,异面直线 $AD$ 与 $BC$ 所成角的余弦值为 $\dfrac{\sqrt 3 }{6}$.
解法二:
如图,过 $F$ 作 $FM \perp AC$,交 $AB$ 于 $M$.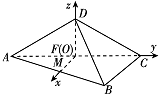 已知 $AD = CD$,平面 $ABC \perp 平面 ACD$,易知 $FC$,$FD$,$FM$ 两两垂直.
已知 $AD = CD$,平面 $ABC \perp 平面 ACD$,易知 $FC$,$FD$,$FM$ 两两垂直.
以 $F$ 为原点,射线 $FM$,$FC$,$FD$ 分别为 $x$ 轴,$y$ 轴,$z$ 轴的正半轴,建立空间直角坐标系 $O - xyz$.
不妨设 $AD = 2$,由 $CD = AD$,$ \angle CAD = 30^\circ$,易知点 $A$,$C$,$D$ 的坐标分别为\[A\left( {0, - \sqrt 3 ,0} \right),C\left( {0,\sqrt 3 ,0} \right),D\left( {0,0,1} \right),\]则 $\overrightarrow {AD} = \left( {0,\sqrt 3 ,1} \right)$.显然向量 $\overrightarrow k = \left( {0,0,1} \right)$ 是平面 $ABC$ 的法向量.
已知二面角 $C - AB - D$ 为 $60^\circ $,故可取平面 $ABD$ 的单位法向量 $\overrightarrow n = \left( {l,m,n} \right)$.
使得 $ \left\langle \overrightarrow n ,\overrightarrow k \right\rangle = 60^\circ$,从而\[n = \dfrac{1}{2}.\]由 $\overrightarrow n \perp \overrightarrow {AD} $,有 $\sqrt 3 m + n = 0$,从而 $m = - \dfrac{\sqrt 3 }{6}$.
由 ${l^2} + {m^2} + {n^2} = 1$,得 $l = \pm \dfrac{\sqrt 6 }{3}$.
设点 $B$ 的坐标为 $B\left( {x,y,0} \right)$,由 $\overrightarrow {AB} \perp \overrightarrow {BC} $,$\overrightarrow n \perp \overrightarrow {AB} $,取 $l = \dfrac{\sqrt 6 }{3}$ 有\[ \begin{cases}
{x^2} + {y^2} = 3, \\
\dfrac{\sqrt 6 }{3}x - \dfrac{\sqrt 3 }{6}\left( {y + \sqrt 3 } \right) = 0, \\
\end{cases} \]解得\[ \begin{cases}x = \dfrac{4\sqrt 6 }{9}, \\
y = \dfrac{7\sqrt 3 }{9}, \\
\end{cases} 或 \begin{cases}x = 0, \\
y = - \sqrt 3, \\
\end{cases} \left(舍去\right).\]易知 $l = - \dfrac{\sqrt 6 }{3}$ 与坐标系的建立方式不合,舍去.
因此点 $B$ 的坐标为 $B\left( {\dfrac{4\sqrt 6 }{9},\dfrac{7\sqrt 3 }{9},0} \right)$,所以\[\overrightarrow {CB} = \left( {\dfrac{4\sqrt 6 }{9}, - \dfrac{2\sqrt 3 }{9},0} \right).\]从而\[ \begin{split}\cos \left\langle \overrightarrow {AD} \cdot \overrightarrow {CB} \right\rangle & = \dfrac{{\overrightarrow {AD} \cdot \overrightarrow {CB} }}{{\left| {\overrightarrow {AD} } \right|\left| {\overrightarrow {CB} } \right|}} \\& = \dfrac{{\sqrt 3 \left( { - \dfrac{2\sqrt 3 }{9}} \right)}}{{\sqrt {3 + 1} \sqrt {{{\left( {\dfrac{4\sqrt 6 }{9}} \right)}^2} + {{\left( { - \dfrac{2\sqrt 3 }{9}} \right)}^2}} }} \\& = - \dfrac{\sqrt 3 }{6},\end{split} \]故异面直线 $AD$ 与 $BC$ 所成的角的余弦值为 $\dfrac{\sqrt 3 }{6}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2