如图,直线 $ l:y=x+b $ 与抛物线 $ C:{{x}^{2}}=4y $ 相切于点 $ A $.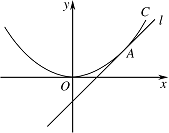

【难度】
【出处】
2011年高考福建卷(文)
【标注】
-
求实数 $ b $ 的值;标注答案略解析由\[ \begin{cases}
y=x+b ,\\
{{x}^{2}}=4y ,\\
\end{cases}\]得\[{{x}^{2}}-4x-4b=0, \quad \cdots \cdots ① \]因为直线 $l$ 与抛物线 $C$ 相切,所以\[\Delta ={{\left( -4 \right)}^{2}}-4\times \left( -4b \right)=0.\]解得 $b=-1$. -
求以点 $ A $ 为圆心,且与抛物线 $ C $ 的准线相切的圆的方程.标注答案略解析由(1)可知 $ b=-1 $,故方程 $ ① $ 即为\[{{x}^{2}}-4x+4=0.\]解得 $ x=2 $,代入 $ {{x}^{2}}=4y $,得 $ y=1 $,故点 $ A\left( 2,1 \right) $.
因为圆 $ A $ 与抛物线 $ C $ 的准线相切,
所以圆 $ A $ 的半径 $ r $ 等于圆心 $ A $ 到抛物线的准线 $ y=-1 $ 的距离.
即\[r=\left| 1-\left( -1 \right) \right|=2,\]所以圆 $ A $ 的方程为\[{{\left( x-2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=4.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2