如图,四棱锥 $P-ABCD$ 中,$PA\perp 底面 ABCD$,$AB\perp AD $,点 $E$ 在线段 $AD $ 上,且 $CE\parallel AB$.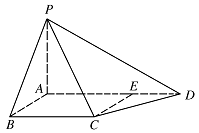

【难度】
【出处】
2011年高考福建卷(文)
【标注】
-
求证:$ CE\perp 平面 PAD $;标注答案略解析因为 $ PA\perp 平面 ABCD $,$ CE\subset 平面 ABCD $.
所以 $ PA\perp CE $.
因为 $ AB\perp AD $,$ CE\parallel AB $,所以 $ CE\perp AD $.
又 $ PA\cap AD=A $,所以 $ CE\perp 平面 PAD $. -
若 $ PA=AB=1 $,$ AD=3 $,$ CD=\sqrt{2} $,$ \angle CDA=45^\circ $,求四棱锥 $ P-ABCD $ 的体积.标注答案略解析由(1)可知 $ CE\perp AD $.
在 $ {\mathrm{Rt}}\triangle ECD $ 中,$ DE=CD\cdot \cos 45{}^\circ =1 $,$ CE=CD\cdot \sin 45{}^\circ =1 $.
又因为 $ AB=CE=1 $,$ AB\parallel CE $,$AB\perp AD $.
所以四边形 $ ABCE $ 为矩形.
所以\[\begin{split}{{S}_{四边形 ABCD}} & ={{S}_{四边形 ABCE}}+{{S}_{\triangle ECD}} \\& =AB\cdot AE+\frac{1}{2}CE\cdot DE \\& =1\times 2+\frac{1}{2}\times 1\times 1=\frac{5}{2}.\end{split}\]又 $ PA\perp 平面 ABCD $,$ PA=1 $.
所以\[{{V}_{P-ABCD}}=\frac{1}{3}{{S}_{四边形 ABCD}}\cdot PA=\frac{1}{3}\times \frac{5}{2}\times 1=\frac{5}{6}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2