设函数 $ f\left( \theta \right)=\sqrt{3}\sin \theta +\cos \theta $，其中，角 $ \theta $ 的顶点与坐标原点重合，始边与 $ x $ 轴非负半轴重合，终边经过点 $ P\left( x, y \right) $，且 $ 0\leqslant \theta \leqslant {\rm{\pi}} $．
【难度】
【出处】
2011年高考福建卷（文）
【标注】
-
若点 $ P $ 的坐标为 $ \left( \dfrac{1}{2}, \dfrac{\sqrt{3}}{2} \right) $，求 $ f\left( \theta \right) $ 的值；标注答案略解析由点 $ P $ 的坐标和三角函数的定义可得\[ \begin{cases}
\sin \theta =\dfrac{\sqrt{3}}{2}, \\
\cos \theta =\dfrac{1}{2}, \\
\end{cases} \]于是\[ f\left( \theta \right)=\sqrt{3}\sin \theta +\cos \theta =\sqrt{3}\times \frac{\sqrt{3}}{2}+\frac{1}{2}=2.\] -
若点 $ P\left( x, y \right) $ 为平面区域 $\varOmega : \begin{cases}
x+y\geqslant 1 \\
x\leqslant 1 \\
y\leqslant 1 \\
\end{cases}$ 上的一个动点，试确定角 $ \theta $ 的取值范围，并求函数 $ f\left( \theta \right) $ 的最小值和最大值．标注答案略解析作出平面区域 $ \varOmega $（即三角形区域 $ ABC $）如图所示，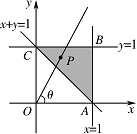
其中 $ A\left( 1, 0 \right) $，$ B\left( 1,1 \right) $，$ C\left( 0,1 \right) $．于是 $ 0\leqslant \theta \leqslant \dfrac{ {\rm{\pi}}}{2} $．
又\[f\left( \theta \right)=\sqrt{3}\sin \theta +\cos \theta =2\sin \left( \theta +\frac{ {\mathrm{\pi}} }{6} \right),\]且 $\dfrac{{\mathrm{ \pi }}}{6}\leqslant \theta +\dfrac{{\mathrm{\pi}}}{6}\leqslant \dfrac{2 {\mathrm{\pi}} }{3}$，故
当 $ \theta +\dfrac{{\rm{\pi}}}{6}=\dfrac{{\rm{\pi}}}{2} $，即 $ \theta =\dfrac{ {\mathrm{\pi }}}{3} $ 时，$ f\left( \theta \right) $ 取得最大值，且最大值等于 $ 2 $；
当 $ \theta +\dfrac{{\mathrm{\pi}}}{6}=\dfrac{{\mathrm{\pi}}}{6} $，即 $ \theta =0$ 时，$ f\left( \theta \right) $ 取得最小值，且最小值等于 $ 1 $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
