如图,四棱锥 $P - ABCD$ 中,$PA \perp 底面 ABCD$,四边形 $ABCD$ 中,$AB \perp AD$,$AB + AD = 4$,$CD = \sqrt 2 $,$ \angle CDA = 45^\circ $.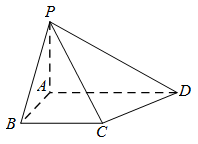

【难度】
【出处】
2011年高考福建卷(理)
【标注】
-
求证:平面 $PAB \perp 平面 PAD$;标注答案略解析因为 $PA \perp 平面 ABCD$,$AB \subset 平面 ABCD$,所以 $PA \perp AB$.
又 $AB \perp AD$,$PA \cap AD = A$,所以 $AB \perp 平面 PAD$.
又 $AB \subset 平面 PAB$,所以平面 $PAB \perp 平面 PAD$. -
设 $AB = AP$.
① 若直线 $PB$ 与平面 $PCD$ 所成的角为 $30^\circ $,求线段 $AB$ 的长;
② 在线段 $AD$ 上是否存在一个点 $G$,使得点 $G$ 到点 $P$,$B$,$C$,$D$ 的距离都相等?说明理由.标注答案略解析① 以 $A$ 为坐标原点,建立空间直角坐标系 $A - xyz$(如图).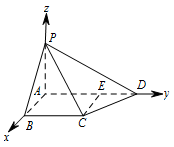 在平面 $ABCD$ 内,作 $CE\parallel AB$ 交 $AD$ 于点 $E$,则 $CE \perp AD$.
在平面 $ABCD$ 内,作 $CE\parallel AB$ 交 $AD$ 于点 $E$,则 $CE \perp AD$.
在 ${\mathrm{Rt}}\triangle CDE$ 中,\[\begin{split}DE &= CD \cdot \cos 45^\circ = 1 , \\ CE &= CD \cdot \sin 45^\circ = 1.\end{split}\]设 $AB = AP = t$,则\[B\left( {t,0,0} \right),P\left( {0,0,t} \right).\]由 $AB + AD = 4$,得\[AD = 4 - t,\]所以\[E\left( {0,3 - t,0} \right),C\left( {1,3 - t,0} \right),D\left( {0,4 - t,0} \right),\]从而\[\begin{split}\overrightarrow {CD} &= \left( { - 1,1,0} \right), \\ \overrightarrow {PD} &= \left( {0,4 - t, - t} \right).\end{split}\]① 设平面 $PCD$ 的法向量为 $\overrightarrow n = \left( {x,y,z} \right)$,由\[\overrightarrow n \perp \overrightarrow {CD} ,\overrightarrow n \perp \overrightarrow {PD} ,\]得\[\begin{cases}- x + y = 0, \\
\left( {4 - t} \right)y - tz = 0 ,\\
\end{cases}\]取 $x = t$,得平面 $PCD$ 的一个法向量\[\overrightarrow n = \left( {t,t,4 - t} \right).\]又 $\overrightarrow {PB} = \left( {t,0, - t} \right)$,故由直线 $PB$ 与平面 $PCD$ 所成的角为 $30^\circ $,得\[\cos 60^\circ = \left| {\dfrac{{\overrightarrow n \cdot \overrightarrow {PB} }}{{\left| {\overrightarrow n } \right| \cdot \left| {\overrightarrow {PB} } \right|}}} \right|,\]即\[\dfrac{{\left| {2{t^2} - 4t} \right|}}{{\sqrt {{t^2} + {t^2} + {{\left( {4 - t} \right)}^2}} \cdot \sqrt {2{t^2}} }} = \dfrac{1}{2},\]解得\[t = \dfrac{4}{5} 或 t = 4 \left(舍去,因为 AD = 4 - t > 0 \right) ,\]所以\[AB = \dfrac{4}{5}.\]② 解法一:
假设在线段 $AD$ 上存在一个点 $G$,使得点 $G$ 到点 $P$,$B$,$C$,$D$ 的距离都相等.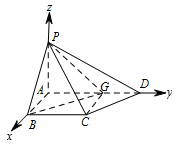 设 $G\left( {0,m,0} \right)$(其中 $0 \leqslant m \leqslant 4 - t$),则\[\begin{split}\overrightarrow {GC} & = \left( {1,3 - t - m,0} \right), \\ \overrightarrow {GD} & = \left( {0,4 - t - m,0} \right), \\ \overrightarrow {GP} & = \left( {0, - m,t} \right).\end{split}\]由 $\left| {\overrightarrow {GC} } \right| = \left| {\overrightarrow {GD} } \right|$,得\[{1^2} + {\left( {3 - t - m} \right)^2} = {\left( {4 - t - m} \right)^2},\]即\[t = 3 - m, \quad \cdots \cdots ① \]由 $\left| {\overrightarrow {GD} } \right| = \left| {\overrightarrow {GP} } \right|$,得\[{\left( {4 - t - m} \right)^2} = {m^2} + {t^2}, \quad \cdots \cdots ② \]由 $ ① $ $ ② $ 消去 $t$,化简得\[{m^2} - 3m + 4 = 0, \quad \cdots \cdots ③ \]由于方程 $ ③ $ 没有实数根,所以线段 $AD$ 上不存在一个点 $G$,使得点 $G$ 到点 $P$,$C$,$D$ 的距离都相等,从而,在线段 $AD$ 上不存在一个点 $G$,使得点 $G$ 到点 $P$,$B$,$C$,$D$ 的距离都相等.
设 $G\left( {0,m,0} \right)$(其中 $0 \leqslant m \leqslant 4 - t$),则\[\begin{split}\overrightarrow {GC} & = \left( {1,3 - t - m,0} \right), \\ \overrightarrow {GD} & = \left( {0,4 - t - m,0} \right), \\ \overrightarrow {GP} & = \left( {0, - m,t} \right).\end{split}\]由 $\left| {\overrightarrow {GC} } \right| = \left| {\overrightarrow {GD} } \right|$,得\[{1^2} + {\left( {3 - t - m} \right)^2} = {\left( {4 - t - m} \right)^2},\]即\[t = 3 - m, \quad \cdots \cdots ① \]由 $\left| {\overrightarrow {GD} } \right| = \left| {\overrightarrow {GP} } \right|$,得\[{\left( {4 - t - m} \right)^2} = {m^2} + {t^2}, \quad \cdots \cdots ② \]由 $ ① $ $ ② $ 消去 $t$,化简得\[{m^2} - 3m + 4 = 0, \quad \cdots \cdots ③ \]由于方程 $ ③ $ 没有实数根,所以线段 $AD$ 上不存在一个点 $G$,使得点 $G$ 到点 $P$,$C$,$D$ 的距离都相等,从而,在线段 $AD$ 上不存在一个点 $G$,使得点 $G$ 到点 $P$,$B$,$C$,$D$ 的距离都相等.
解法二:
假设在线段 $AD$ 上存在一个点 $G$,使得点 $G$ 到点 $P$,$B$,$C$,$D$ 的距离都相等.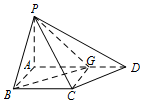 由 $GC = GD$,得\[\angle GCD = \angle GDC = 45^\circ ,\]从而\[\angle CGD = 90^\circ ,\]所以\[GD = CD \cdot \cos 45^\circ = 1.\]设 $AB = \lambda $,则\[\begin{split}AD & = 4 - \lambda , \\ AG & = AD - GD = 3 - \lambda .\end{split}\]在 ${\mathrm{Rt}}\triangle ABG$ 中,\[\begin{split}GB & = \sqrt {{AB}^2 + A{G^2}} \\&
由 $GC = GD$,得\[\angle GCD = \angle GDC = 45^\circ ,\]从而\[\angle CGD = 90^\circ ,\]所以\[GD = CD \cdot \cos 45^\circ = 1.\]设 $AB = \lambda $,则\[\begin{split}AD & = 4 - \lambda , \\ AG & = AD - GD = 3 - \lambda .\end{split}\]在 ${\mathrm{Rt}}\triangle ABG$ 中,\[\begin{split}GB & = \sqrt {{AB}^2 + A{G^2}} \\&
= \sqrt {{\lambda ^2} + {{\left( {3 - \lambda } \right)}^2}} \\& = \sqrt {2{{\left( {\lambda - \dfrac{3}{2}} \right)}^2} + \dfrac{9}{2}} > 1,\end{split}\]这与 $GB = GD$ 矛盾,所以在线段 $AD$ 上不存在一个点 $G$,使得点 $G$ 到点 $B$,$C$,$D$ 的距离都相等,从而,在线段 $AD$ 上不存在一个点 $G$,使得点 $G$ 到点 $P$,$B$,$C$,$D$ 的距离都相等.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2