如图,已知正三棱柱 $ ABC-A_1B_1C_1 $ 的各棱长都是 $ 4 $,$ E $ 是 $ BC $ 的中点,动点 $ F $ 在侧棱 $ CC_1 $ 上,且不与点 $ C $ 重合.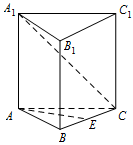

【难度】
【出处】
2011年高考湖北卷(理)
【标注】
-
当 $ CF=1 $ 时,求证:$ EF\perp A_1C $;标注答案略解析过 $ E $ 作 $ EN\perp AC $ 于 $ N $,连接 $ EF $.
解法一:如图,连接 $ NF $,$ AC_1 $,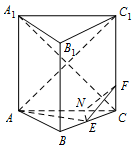 由正三棱柱的性质知,底面 $ ABC\perp 侧面A_1C $,
由正三棱柱的性质知,底面 $ ABC\perp 侧面A_1C $,
又底面 $ ABC\cap 侧面A_1C=AC $,且 $ EN \subset$ 底面 $ ABC $,
所以 $ EN\perp $ 侧面 $ A_1C $,$ NF $ 为 $ EF $ 在侧面 $ A_1C $ 内的射影.
在 $ {\mathrm{Rt}}\triangle CNE $ 中,$ CN=CE\cos 60^\circ =1 $.
则由 $ {\dfrac{CF}{CC_1}}={\dfrac{CN}{CA}}={\dfrac{1}{4}} $,得 $ NF\parallel AC_1 $,
又 $ AC_1\perp A_1C $,故 $ NF\perp A_1C $.
由三垂线定理知 $ EF\perp A_1C $.
解法二:
建立如图所示的空间直角坐标系,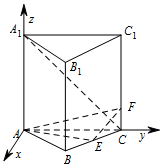 则由已知可得 $ A\left(0,0,0\right) $,$ B\left(2{\sqrt{3}},2,0\right) $,$ C\left(0,4,0\right) $,$ A_1\left(0,0,4\right) $,$ E\left({\sqrt{3}},3,0\right) $,$ F\left(0,4,1\right) $,
则由已知可得 $ A\left(0,0,0\right) $,$ B\left(2{\sqrt{3}},2,0\right) $,$ C\left(0,4,0\right) $,$ A_1\left(0,0,4\right) $,$ E\left({\sqrt{3}},3,0\right) $,$ F\left(0,4,1\right) $,
于是 $ {\overrightarrow {CA_1}}=\left(0,-4,4\right) $,$ {\overrightarrow {EF}}=\left(-{\sqrt{3}},1,1\right) $.则\[ \begin{split} {\overrightarrow {CA_1}}\cdot {\overrightarrow {EF}}&=\left(0,-4,4\right)\cdot \left(-{\sqrt{3}},1,1\right)\\&=0-4+4=0 ,\end{split}\]故 $ EF\perp A_1C $. -
设二面角 $ C-AF-E $ 的大小为 $ \theta $,求 $ \tan \theta $ 的最小值.标注答案略解析解法一:
如图,连接 $ AF $,过 $ N $ 作 $ NM\perp AF $ 于 $ M $,连接 $ ME $.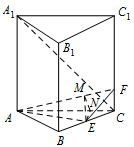 由(1)知 $ EN\perp 侧面 A_1C $,根据三垂线定理得 $ EM\perp AF $,
由(1)知 $ EN\perp 侧面 A_1C $,根据三垂线定理得 $ EM\perp AF $,
所以 $ \angle EMN $ 是二面角 $ C-AF-E $ 的平面角,即 $ \angle EMN=\theta $.
设 $ \angle FAC=\alpha $,则 $ 0^\circ <\alpha \leqslant 45^\circ $.
在 $ {\mathrm{Rt}}\triangle CNE $ 中,$ NE=EC\cdot \sin 60^\circ ={\sqrt{3}} $,
在 ${\mathrm{ Rt}}\triangle AMN $ 中,$ MN=AN\cdot \sin \alpha =3\sin \alpha $,
故 $ \tan \theta ={\dfrac{NE}{MN}}={\dfrac{{\sqrt{3}}}{3\sin \alpha }} $.
又 $ 0^\circ <\alpha \leqslant 45^\circ $,∴ $ 0<\sin \alpha \leqslant {\dfrac{{\sqrt{2}}}{2}} $.
故当 $ \sin \alpha ={\dfrac{{\sqrt{2}}}{2}} $,即 $ \alpha =45^\circ $ 时,$\tan \theta $ 达到最小值,
$ \tan \theta ={\dfrac{{\sqrt{3}}}{3}}\times {\sqrt{2}}={\dfrac{{\sqrt{6}}}{3}} $,此时 $ F $ 与 $ C_1 $ 重合.
解法二:
设 $ CF=\lambda \left(0<\lambda \leqslant 4\right) $,平面 $ AEF $ 的一个法向量为 $\overrightarrow m=\left(x,y,z\right) $,
则由(1)得 $ F\left(0,4,\lambda \right) $,$ {\overrightarrow {AE}}=\left({\sqrt{3}},3,0\right) $,$ {\overrightarrow {AF}}=\left(0,4,\lambda \right) $,
于是由 $ \overrightarrow m\perp {\overrightarrow {AE}} $,$ \overrightarrow m\perp {\overrightarrow {AF}} $,可得\[ \begin{cases}\overrightarrow m·{\overrightarrow {AE}}=0,\\
\overrightarrow m·{\overrightarrow {AF}}=0,\end{cases} \]即\[ \begin{cases} {\sqrt{3}}x+3y=0,\\
4y+\lambda z=0,\end{cases} \]取 $\overrightarrow m=\left({\sqrt{3}}\lambda ,-\lambda ,4\right) $.
又由正三棱柱的性质可取侧面 $ AC_1 $ 的一个法向量为 $\overrightarrow n=\left(1,0,0\right) $,
于是由 $ \theta $ 为锐角可得\[\begin{split}\cos \theta &={\dfrac{ \left|\overrightarrow m\cdot \overrightarrow n \right|}{ \left|\overrightarrow m \right|\cdot \left|\overrightarrow n \right|}}={\dfrac{{\sqrt{3}}\lambda }{2{\sqrt{\lambda ^2+4}}}} ,\\ \sin \theta &={\dfrac{{\sqrt{\lambda^ 2+16}}}{2{\sqrt{\lambda ^2+4}}}} ,\end{split}\]所以\[ \tan \theta ={\dfrac{{\sqrt{\lambda ^2+16}}}{{\sqrt{3}}\lambda }}={\sqrt{{\dfrac{1}{3}}+{\dfrac{16}{3\lambda^ 2}}}} .\]由 $ 0<\lambda \leqslant 4 $,得 $ {\dfrac{1}{\lambda }}\geqslant {\dfrac{1}{4}} $,即\[ \tan \theta \geqslant {\sqrt{{\dfrac{1}{3}}+{\dfrac{1}{3}}}}={\dfrac{{\sqrt{6}}}{3}} ,\]故当 $ \lambda =4 $,即点 $ F $ 与点 $ C_1 $ 重合时,$ \tan \theta $ 取得最小值 $ {\dfrac{{\sqrt{6}}}{3}} $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2