题目 如图，四棱锥 $V-ABCD$ 的底面是矩形 $ABCD$，$\triangle VAB$ 是等边三角形，$AB=a,BC=2a$，二面角 $V-AB-C$ 的余弦值为 $\dfrac{\sqrt3}{3}$，$M,N$ 分别是 $AD$，$BC$ 的中点． 问题1 求证：$BM\perp$ 平面 $VAN$； 答案1 略 解析1 记 $AN$ 与 $BM$ 交点为 $O$，取 $AB$ 中点 $E$，如图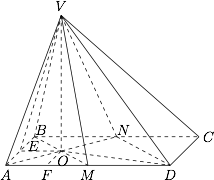．<img src="/static/images/2b4494cee0cb7856f97e85c81a7184e7.png" class="img-responsive" />易知 $\angle VEO$ 即二面角 $V-AB-C$ 的平面角，又$$EO=\dfrac12 a,VE=\dfrac{\sqrt3}{2}a,$$在 $\triangle VEO$ 中解三角形得 $\angle VOE=\dfrac{\pi}{2},$ 故 $OV\perp OE$，又由于$$\begin{cases} AB\perp VE,\\AB\perp OE,\\ VE\cap OE=E,\end{cases}$$所以 $AB\perp$ 面 $VOE$，又 $VO\subset$ 面 $VOE$ 内，所以 $OV\perp AB$．因此 $OV\perp$ 面 $ABCD$．又因为 $BM\subset$ 面 $ABCD$，故$$BM\perp AN,$$于是 $BM\perp$ 面 $VAN$． 备注1 问题2 求 $BM$ 与 $VD$ 所成角的余弦值； 答案2 $\dfrac{\sqrt3}{3}$ 解析2 由于 $ND\parallel BM$，故即求 $ND$ 与 $VD$ 夹角．易得$$\left(ND=\sqrt2a\right)\land\left(VN=a\right)$$又$$VD=\sqrt{VO^2+OD^2}=\sqrt{VE^2-EO^2+OF^2+FD^2}=\sqrt3a,$$于是 $\triangle VND$ 中，$\angle VND=\dfrac {\pi}2$ 且 $\cos \angle VDN=\dfrac{\sqrt3}{3}$，因此所求两直线夹角余弦值为 $\dfrac{\sqrt3}3$． 备注2 问题3 求点 $C$ 到平面 $VAB$ 的距离． 答案3 $2a$ 解析3 略 备注3 记三棱锥 $V-ABC$ 的体积为 $V$，则$$V=\dfrac13\cdot VO\cdot S_{\triangle ABC}=\dfrac13\cdot \dfrac{\sqrt2}{2}a\cdot\dfrac12\cdot a\cdot 2a=\dfrac{\sqrt2}6a^3,$$若设点 $C$ 到平面 $VAB$ 的距离为 $h$，则$$V=\dfrac13\cdot h\cdot S_{\triangle VAB}=\dfrac13\cdot h\cdot\dfrac{\sqrt3}4a^2.$$联立上式解得 $h=\dfrac{2\sqrt6}{3}a$．因此点 $C$ 到平面 $VAB$ 的距离为 $\dfrac{2\sqrt6}{3}a$．