如图,四棱锥 $S - ABCD$ 中,$AB\parallel CD$,$BC \perp CD$,侧面 $SAB$ 为等边三角形,$AB = BC = 2$,$CD = SD = 1$.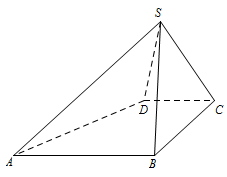

【难度】
【出处】
2011年高考大纲全国卷(理)
【标注】
-
证明:$SD \perp 平面 SAB$;标注答案略解析解法一:
取 $AB$ 中点 $E$,连结 $DE$,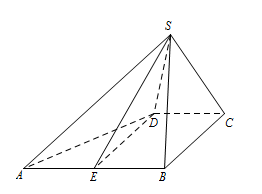 则四边形 $BCDE$ 为矩形,\[DE = CB = 2,\]连结 $SE$,则 $SE \perp AB$,\[SE = \sqrt 3 .\]又 $SD = 1$,故\[E{D^2} = S{E^2} + S{D^2},\]所以 $\angle DSE$ 为直角.
则四边形 $BCDE$ 为矩形,\[DE = CB = 2,\]连结 $SE$,则 $SE \perp AB$,\[SE = \sqrt 3 .\]又 $SD = 1$,故\[E{D^2} = S{E^2} + S{D^2},\]所以 $\angle DSE$ 为直角.
由 $AB \perp DE$,$AB \perp SE$,$DE \cap SE = E$,得 $AB \perp $ 平面 $SDE$,所以 $AB \perp SD$.
$SD$ 与两条相交直线 $AB,SE$ 都垂直.所以 $SD \perp $ 平面 $SAB$.
另解:由已知易求得\[SD = 1,AD = \sqrt 5 ,SA = 2,\]于是\[S{A^2} + S{D^2} = A{D^{^2}}.\]可知 $SD \perp SA$,
同理可得 $SD \perp SB$,又 $SA \cap SB = S$.所以 $SD \perp $ 平面 $SAB$.
解法二:
以 $C$ 为原点,射线 $CD$ 为 $x$ 轴的正半轴,建立如图所示的空间直角坐标系 $C - xyz$.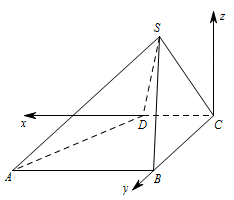 设 $D\left(1,0,0\right)$,则 $A\left(2,2,0\right) , B\left(0,2,0\right).$ 又设 $S\left(x,y,z\right)$,则 $x > 0,y > 0,z > 0$.\[\begin{split}\overrightarrow {AS} & = \left(x - 2,y - 2,z\right), \\ \overrightarrow {BS} & = \left(x,y - 2,z\right), \\ \overrightarrow {DS} & = \left(x - 1,y,z\right),\end{split}\]由 $ \left|\overrightarrow {AS} \right| = \left|\overrightarrow {BS} \right|$ 得\[\sqrt {{{\left(x - 2\right)}^2} + {{\left(y - 2\right)}^2} + {z^2}} = \sqrt {{x^2} + {{\left(y - 2\right)}^2} + {z^2}} ,\]故\[x = 1.\]由 $ \left|\overrightarrow {DS} \right| = 1,$ 得\[{y^2} + {z^2} = 1,\]又由 $|\overrightarrow {BS} | = 2,$ 得\[{x^2} + {\left(y - 2\right)^2} + {z^2} = 4,\]即\[{y^2} + {z^2} - 4y + 1 = 0,\]故\[y = \dfrac{1}{2},z = \dfrac{{\sqrt 3 }}{2}.\]于是 $S\left( {1,\dfrac{1}{2},\dfrac{{\sqrt 3 }}{3}} \right)$,\[\begin{split} \overrightarrow {AS} & = \left( { - 1, - \dfrac{3}{2},\dfrac{{\sqrt 3 }}{2}} \right), \\ \overrightarrow {BS} & = \left( {1, - \dfrac{3}{2},\dfrac{{\sqrt 3 }}{2}} \right), \\ \overrightarrow {DS} &= \left( {0,\dfrac{1}{2},\dfrac{{\sqrt 3 }}{2}} \right), \end{split} \]所以\[\begin{split} \overrightarrow {DS} \cdot \overrightarrow {AS} & = 0, \\ \overrightarrow {DS} \cdot \overrightarrow {BS} & = 0. \end{split} \]故 $DS \perp AS,DS \perp BS$,又 $AS \cap BS = S$,所以 $SD \perp $ 平面 $SAB$.
设 $D\left(1,0,0\right)$,则 $A\left(2,2,0\right) , B\left(0,2,0\right).$ 又设 $S\left(x,y,z\right)$,则 $x > 0,y > 0,z > 0$.\[\begin{split}\overrightarrow {AS} & = \left(x - 2,y - 2,z\right), \\ \overrightarrow {BS} & = \left(x,y - 2,z\right), \\ \overrightarrow {DS} & = \left(x - 1,y,z\right),\end{split}\]由 $ \left|\overrightarrow {AS} \right| = \left|\overrightarrow {BS} \right|$ 得\[\sqrt {{{\left(x - 2\right)}^2} + {{\left(y - 2\right)}^2} + {z^2}} = \sqrt {{x^2} + {{\left(y - 2\right)}^2} + {z^2}} ,\]故\[x = 1.\]由 $ \left|\overrightarrow {DS} \right| = 1,$ 得\[{y^2} + {z^2} = 1,\]又由 $|\overrightarrow {BS} | = 2,$ 得\[{x^2} + {\left(y - 2\right)^2} + {z^2} = 4,\]即\[{y^2} + {z^2} - 4y + 1 = 0,\]故\[y = \dfrac{1}{2},z = \dfrac{{\sqrt 3 }}{2}.\]于是 $S\left( {1,\dfrac{1}{2},\dfrac{{\sqrt 3 }}{3}} \right)$,\[\begin{split} \overrightarrow {AS} & = \left( { - 1, - \dfrac{3}{2},\dfrac{{\sqrt 3 }}{2}} \right), \\ \overrightarrow {BS} & = \left( {1, - \dfrac{3}{2},\dfrac{{\sqrt 3 }}{2}} \right), \\ \overrightarrow {DS} &= \left( {0,\dfrac{1}{2},\dfrac{{\sqrt 3 }}{2}} \right), \end{split} \]所以\[\begin{split} \overrightarrow {DS} \cdot \overrightarrow {AS} & = 0, \\ \overrightarrow {DS} \cdot \overrightarrow {BS} & = 0. \end{split} \]故 $DS \perp AS,DS \perp BS$,又 $AS \cap BS = S$,所以 $SD \perp $ 平面 $SAB$. -
求 $AB$ 与平面 $SBC$ 所成角的大小.标注答案略解析解法一:
由 $AB \perp $ 平面 $SDE$ 知,平面 $ABCD \perp $ 平面 $SDE$.
作 $SF \perp DE$,垂足为 $F$,则 $SF \perp $ 平面 $ABCD$,\[SF = \dfrac{{SD \times SE}}{{DE}} = \dfrac{{\sqrt 3 }}{2}.\]作 $FG \perp BC$,垂足为 $G$,则\[FG = DC = 1.\]连结 $SG$.则 $SG \perp BC$.\[SG = \sqrt {S{F^2} + F{G^2}} = \dfrac{{\sqrt 7 }}{2},\]又 $BC \perp FG,SG \cap FG = G$,故 $BC \perp $ 平面 $SFG$,平面 $SBC \perp $ 平面 $SFG$.
作 $FH \perp SG$,$H$ 为垂足,则 $FH \perp $ 平面 $SBC$.\[FH = \dfrac{{SF \times FG}}{{SG}} = \dfrac{{\sqrt 3 }}{{\sqrt 7 }},\]即 $F$ 到平面 $SBC$ 的距离为 $\dfrac{{\sqrt {21} }}{7}$.
由于 $ED\parallel BC$,所以 $ED\parallel $ 平面 $SBC$,$E$ 到平面 $SBC$ 的距离 $d$ 也为 $\dfrac{{\sqrt {21} }}{7}$.
设 $AB$ 与平面 $SBC$ 所成的角为 $\alpha $,则\[\sin \alpha = \dfrac{d}{{EB}} = \dfrac{{\sqrt {21} }}{7},\alpha = \arcsin \dfrac{{\sqrt {21} }}{7}.\]解法二: 设平面 $SBC$ 的法向量 $\overrightarrow a = \left(m,n,p\right)$,则 $\overrightarrow a \perp \overrightarrow {BS} ,\overrightarrow a \perp \overrightarrow {CB} ,$ 所以\[\begin{split} \overrightarrow a \cdot \overrightarrow {BS} & = 0, \\ \overrightarrow a \cdot \overrightarrow {CB} & = 0.\end{split} \]又\[\begin{split}\overrightarrow {BS} & = \left( {1, - \dfrac{3}{2},\dfrac{{\sqrt 3 }}{2}} \right) , \\ \overrightarrow {CB} & = \left(0,2,0\right),\end{split}\]故\[{\begin{cases}m - \dfrac{3}{2}n + \dfrac{{\sqrt 3 }}{2}p = 0, \\
设平面 $SBC$ 的法向量 $\overrightarrow a = \left(m,n,p\right)$,则 $\overrightarrow a \perp \overrightarrow {BS} ,\overrightarrow a \perp \overrightarrow {CB} ,$ 所以\[\begin{split} \overrightarrow a \cdot \overrightarrow {BS} & = 0, \\ \overrightarrow a \cdot \overrightarrow {CB} & = 0.\end{split} \]又\[\begin{split}\overrightarrow {BS} & = \left( {1, - \dfrac{3}{2},\dfrac{{\sqrt 3 }}{2}} \right) , \\ \overrightarrow {CB} & = \left(0,2,0\right),\end{split}\]故\[{\begin{cases}m - \dfrac{3}{2}n + \dfrac{{\sqrt 3 }}{2}p = 0, \\
2n = 0, \\
\end{cases}}\]取 $p = 2$ 得\[\overrightarrow a = \left( { - \sqrt 3 ,0,2} \right),\]又 $\overrightarrow {AB} = \left( - 2,0,0\right)$,所以\[\cos \left\langle \overrightarrow {AB} ,\overrightarrow a \right\rangle = \dfrac{{\overrightarrow {AB} \cdot \overrightarrow a }}{{ \left|\overrightarrow {AB} \right| \cdot \left|\overrightarrow a \right|}} = \dfrac{{\sqrt {21} }}{7}.\]故 $AB$ 与平面 $SBC$ 所成的角为 $\arcsin \dfrac{{\sqrt {21} }}{7}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2