如图，四棱锥 $P - ABCD$ 中，底面 $ABCD$ 为平行四边形，$\angle DAB = 60^\circ $，$AB = 2AD$，$PD \perp 底面 ABCD$．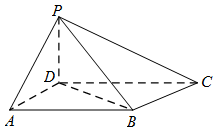
【难度】
【出处】
2011年高考新课标全国卷（理）
【标注】
-
证明：$PA \perp BD$；标注答案略解析因为 $\angle DAB = 60^\circ $，$AB = 2AD$，由余弦定理得\[BD = \sqrt 3 AD,\]从而\[{BD}^2 + {AD}^2 = {AB}^2,\]故 $BD \perp AD$．
又 $PD \perp 底面 ABCD$，可得 $BD \perp PD$．
所以 $BD \perp 平面 PAD$．故 $PA \perp BD$． -
若 $PD = AD$，求二面角 $A - PB - C$ 的余弦值．标注答案略解析如图，以 $D$ 为坐标原点，$AD$ 的长为单位长，射线 $DA$ 为 $x$ 轴的正半轴建立空间直角坐标系 $D - xyz$，
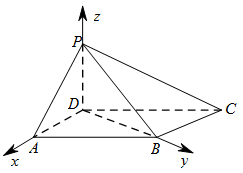则 $A\left(1,0,0\right)$，$B\left( {0,\sqrt 3 ,0} \right)$，$C\left( { - 1,\sqrt 3 ,0} \right)$，$P\left(0,0,1\right)$，故\[\begin{split} \overrightarrow {AB} = \left( { - 1,\sqrt 3 ,0} \right),\overrightarrow {PB} = \left( {0,\sqrt 3 , - 1} \right), \overrightarrow {BC} = \left( - 1,0,0\right).\end{split}\]设平面 $PAB$ 的法向量为 $\overrightarrow n = \left(x,y,z\right)$，则\[\begin{cases}\overrightarrow n \cdot \overrightarrow {AB} = 0, \\
\overrightarrow n \cdot \overrightarrow {PB} = 0. \\
\end{cases}\]即\[\begin{cases}- x + \sqrt 3 y = 0 ,\\
\sqrt 3 y - z = 0 .\\
\end{cases}\]因此可取\[\overrightarrow n = \left( {\sqrt 3 ,1,\sqrt 3 } \right).\]设平面 $PBC$ 的法向量为 $\overrightarrow m $，则\[\begin{cases}\overrightarrow m \cdot \overrightarrow {PB} = 0, \\
\overrightarrow m \cdot \overrightarrow {BC} = 0. \\
\end{cases}\]可取\[\overrightarrow m = \left( {0, - 1, - \sqrt 3 } \right),\]所以\[\cos \left\langle {\overrightarrow m ,\overrightarrow n } \right\rangle = \dfrac{ - 4}{2\sqrt 7 } = - \dfrac{2\sqrt 7 }{7}.\]故二面角 $A - PB - C$ 的余弦值为 $ - \dfrac{2\sqrt 7 }{7}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
