如图，四棱锥 $P - ABCD$ 中，底面 $ABCD$ 为平行四边形，$\angle DAB = 60^\circ $，$AB = 2AD$，$PD \perp 底面 ABCD$．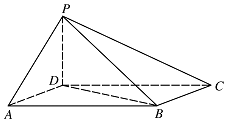
【难度】
【出处】
2011年高考新课标全国卷（文）
【标注】
-
证明：$PA \perp BD$；标注答案略解析因为 $\angle DAB = 60^\circ$，$AB = 2AD$，由余弦定理得\[BD = \sqrt 3 AD,\]从而\[{BD}^2 + {AD}^2 = {AB}^2,\]故 $BD \perp AD$．
又 $PD \perp 底面 ABCD$，可得 $BD \perp PD$，
所以 $BD \perp 平面 PAD$．故 $PA \perp BD$． -
设 $PD = AD = 1$，求棱锥 $D - PBC$ 的高．标注答案略解析如图，作 $DE \perp PB$，垂足为 $E$．
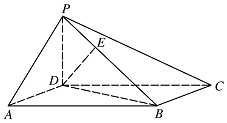已知 $PD \perp 底面 ABCD$，则 $PD \perp BC$．
由（1）知 $BD \perp AD$，
又 $BC\parallel AD$，所以 $BC \perp BD$．
故 $BC \perp 平面 PBD$，$BC \perp DE$．
则 $DE \perp 平面 PBC$．
由题设知，$PD=AD = 1$，则\[BD = \sqrt 3 , PB = 2,\]根据 $DE \cdot PB = PD \cdot BD$，得\[DE = \dfrac{\sqrt 3 }{2},\]即棱锥 $D - PBC$ 的高为 $\dfrac{\sqrt 3 }{2}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
