已知 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 是底面边长为 $ 1 $ 的正四棱柱，高 $A{A_1} = 2$，求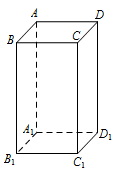
【难度】
【出处】
2011年高考上海卷（文）
【标注】
-
异面直线 $BD$ 与 $A{B_1}$ 所成角的余弦值；标注答案略解析连 $BD$，$ A{B_1} $，$ {B_1}{D_1} $，$A{D_1}$，
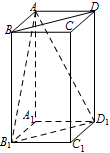因为 $BD\parallel {B_1}{D_1}$，$A{B_1} = A{D_1}$，
所以异面直线 $BD$ 与 $A{B_1}$ 所成角为 $\angle A{B_1}{D_1}$，记 $\angle A{B_1}{D_1} = \theta $，\[AB_1^2 = AD_1^2 = {2^2} + {1^2} = 5, {B_1}D_1^2 = 2,\]所以在 $\triangle A{B_1}{D_1}$ 中，由余弦定理\[\cos \theta = \dfrac{{AB_1^2 + {B_1}D_1^2 - AD_1^2}}{{2A{B_1} \times {B_1}{D_1}}} = \dfrac{{\sqrt {10} }}{10}.\]所以异面直线 $BD$ 与 $A{B_1}$ 所成角的余弦值为 $\dfrac{\sqrt{10}}{10 }$． -
四面体 ${A}{B_1}{D_1}C$ 的体积．标注答案略解析
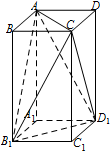连 $AC$，$ C{B_1} $，$C{D_1}$，则所求四面体的体积\[\begin{split}V & = {V_{ABCD - {A_1}{B_1}{C_1}{D_1}}} - 4 \times {V_{C - {B_1}{C_1}{D_1}}} \\& = 2 - 4 \times \dfrac{1}{3} \\& = \dfrac{2}{3}.\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
