在平面直角坐标系 $xOy$ 中，直线 $l: x= - 2 $ 交 $x $ 轴于点 $A$．设 $P $ 是 $l$ 上一点，$M$ 是线段 $OP $ 的垂直平分线上一点，且满足 $\angle MPO = \angle AOP$．
【难度】
【出处】
2011年高考广东卷（文）
【标注】
-
当点 $P$ 在 $l$ 上运动时，求点 $M$ 的轨迹 $E$ 的方程；标注答案略解析如图所示，连接 $OM$，则 ${\left|{PM}\right|} = {\left|{OM}\right|} $．
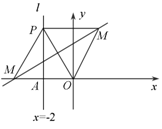因为 $\angle MPO = \angle AOP,$
所以动点 $M$ 满足 $MP \perp l $ 或 $M$ 在 $x$ 的负半轴上，设 $M\left(x,y\right)$．
① 当 $MP \bot l$ 时，$\left| {MP} \right| = \left| {x + 2} \right|,\left| {OM} \right| = \sqrt {{x^2} + {y^2}} $，根据题意有\[ \left| {x + 2} \right| = \sqrt {{x^2} + {y^2}},\]化简得\[{y^2} = 4x + 4\left( {x \geqslant - 1} \right);\]② 当 $M$ 在 $x $ 的负半轴上时，\[y = 0\left( {x < - 1} \right).\]综上所述，点 $M$ 的轨迹 $ E$ 的方程为\[{y^2} = 4x + 4\left( {x \geqslant - 1} \right)\
或 y = 0\left( {x < - 1} \right).\] -
已知 $T\left(1,-1\right) $，设 $H$ 是 $E$ 上动点，求 ${\left|{HO}\right|} + {\left|{HT}\right|} $ 的最小值，并给出此时点 $H$ 的坐标；标注答案略解析由（1）知 $M $ 的轨迹是顶点为 $\left( { - 1,0} \right)$，焦点为原点的抛物线和 $x$ 轴的负半轴上满足 $ y = 0\left( {x < - 1} \right) $ 的点集．
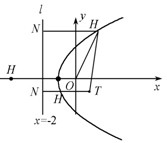① 若 $H$ 是抛物线上的动点，过 $H$ 作 $HN \perp l $ 于 $N$，
由于 $l$ 是抛物线的准线，根据抛物线的定义有 ${\left|{HO}\right|} = {\left|{HN}\right|} $，则\[\left| {HO} \right| + \left| {HT} \right| = \left| {HN} \right| + \left| {HT} \right| .\]当 $N,H,T$ 三点共线时，${\left|{HN}\right|} + {\left|{HT}\right|} $ 有最小值\[\left| {TN} \right| = 3,\]求得此时 $H$ 的坐标为 $\left(-\dfrac 3 4 , -1 \right)$．
② 若 $H$ 是 $x$ 的负半轴 $ y = 0\left( {x < - 1} \right) $ 上的动点显然有\[\left| {HO} \right| + \left| {HT} \right| > 3.\]综上所述，$\left| {HO} \right| + \left| {HT} \right|$ 的最小值为 $3 $，此时点 $H$ 的坐标为 $\left( { - \dfrac{3}{4}, - 1} \right)$． -
过点 $T\left( {1, - 1} \right)$ 且不平行于 $y $ 轴的直线 ${l_1}$ 与轨迹 $E$ 有且只有两个不同的交点，求直线 $l_1 $ 的斜率 $k$ 的取值范围．标注答案略解析如图，
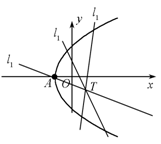设抛物线顶点 $B\left(-1,0\right) $，则直线 $BT$ 的斜率是 ${k_{BT}} = - \dfrac{1}{2}.$
因为点 $T\left(1,-1\right) $ 在抛物线内部，
所以过点 $T$ 且不平行于 $x、y$ 轴的直线 $l_1 $ 必与抛物线有两个交点．
直线 ${l_1}$ 与轨迹 $E$ 的交点个数应当分以下四种情况讨论：
① 当 $k \leqslant - \dfrac 1 2 $ 时，直线 ${l_1}$ 与轨迹 $E$ 有且只有两个不同的交点；
② 当 $- \dfrac 1 2 < k < 0 $ 时，直线 ${l_1}$ 与轨迹 $E$ 有且只有三个不同的交点；
③ 当 $ k = 0 $ 时，直线 ${l_1}$ 与轨迹 $E$ 有且只有一个交点；
④ 当 $ k > 0 $ 时，直线 ${l_1}$ 与轨迹 $E$ 有且只有两个不同的交点．
综上所述，直线 $ l$ 的斜率 $k$ 的取值范围是 $\left( { - \infty , - \dfrac{1}{2}} \right] \cup \left( {0, + \infty } \right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
