如图所示的几何体是将高为 $2 $，底面半径为 $1$ 的直圆柱沿过轴的平面切开后，将其中一半沿切面向右水平平移后得到的．$A,A',B,B'$ 分别为 $\overparen {CD} ,\overparen {C'D'} ,\overparen {DE} ,\overparen {D'E'} $ 的中点，${O_1}$，$ O_1 ' $，${O_2}$，$ O_2 ' $ 分别为 $CD$，$C'D'$，$DE$，$D'E'$ 的中点．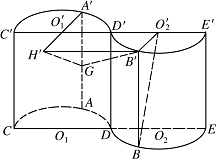
【难度】
【出处】
2011年高考广东卷（文）
【标注】
-
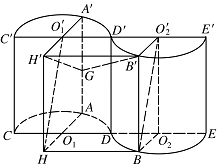
证明：$ O_1 ' ,A',{O_2},B$ 四点共面；标注答案略解析连接 $B{O_2},{O_2} O_2 ' $，
依题意得 ${O_1}$，$ O_1 ' $，${O_2}$，$ O_2 ' $ 是圆柱底面圆的圆心，
即 $CD,C'D',DE,D'E'$ 是圆柱底面圆的直径．
$\because$ $A',B,B'$ 分别为 $\overparen {C'D'}$，$\overparen {DE}$，$\overparen {D'E'}$ 的中点，
$\therefore$ $ \angle A'O_1 ' D' = \angle B'O_2 ' D' = 90^\circ $．
$\therefore$ $A' O_1 ' \parallel B' O_2 ' $．
$\because$ $BB'平行且等于 {O_2} O_2 ' $，四边形 $ {O_2} O_2 'B'B$ 是平行四边形，
$\therefore$ $B {O_2}\parallel B' O_2 ' $，$\therefore$ $A' O_1 ' \parallel B{O_2}$，
$\therefore$ $ O_1 ' ,A', O_2 ,B$ 四点共面． -
设 $G$ 为 $AA'$ 中点，延长 $A' O_1 ' $ 到 $H'$，使得 $ O_1 ' H' = A' O_1 ' $．证明：$B O_2 ' \perp 平面 H'B'G$．标注答案略解析延长 $A{O_1}$ 到 $H$，使得 $O_1 H =A{O_1} $，连接 $HH'$，$H O_1 '$，$HB$，
$\because$ $O_1 'H =A' O_1 '$，
$\therefore$ $ O_1' H' 平行且等于 O_2' B'$，$\therefore$ 四边形 $ O_1' O_2' B'H'$ 是平行四边形，
$\therefore$ $ O_1 ' O_2 ' \parallel H'B $．
$\because$ $ O_1' O_2' \perp{O_2} O_2' , O_1' O_2' \perp B' O_2' ,{O_2} O_2' \cap B' O_2' = O_2' $，
$\therefore$ $ O_1' O_2' \perp 平面 O_2 O_2 ' B' B $，
$\therefore$ $ H'B' \perp $ 平面 ${O_2} O_2' B' B$，
$\because$ $B O_2' \subset 平面 O_2 O_2 ' B'B $，
$\therefore$ $B O_2' \perp H'B'$，
易知四边形 $AA'H'H$ 是正方形，且边长 $AA' = 2 $
$\because$\[\begin{split}\tan \angle H O_1' H' &= \dfrac{{HH'}}{{ O_1' H'}} = 2, \\ \tan \angle A'H'G &= \dfrac{{A'G}}{{A'H'}} = \dfrac{1}{2},\end{split}\]$\therefore$\[\tan \angle H O_1' H' \cdot \tan \angle A'H'G = 1,\]∴ $ \angle H O_1' H' + \angle A'H'G = 90^\circ $，
$\therefore$ $H O_1' \perp H'G$，
易知 $ O_1' O_2' \parallel HB,$ 四边形 $ O_1 ' O_2 ' BH $ 是平行四边形
$\therefore$ $B O_2' \parallel H O_1' $
$\therefore$ $B O_2' \perp H'G$，而 $H'G \cap H'B' = H'$，
$\therefore$ $ BO_2 ' \perp $ 平面 $H'B'G$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
