如图，在锥体 $P - ABCD$ 中，$ABCD$ 是边长为 $1$ 的菱形，且 $\angle DAB = 60^\circ $，$PA = PD = \sqrt 2 $，$PB = 2$，$E$，$F$ 分别是 $BC$，$PC$ 的中点．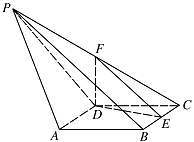
【难度】
【出处】
2011年高考广东卷（理）
【标注】
-
证明：$AD \perp 平面 DEF$；标注答案略解析设 $AD$ 中点为 $H$，连接 $PH$，$BH$．
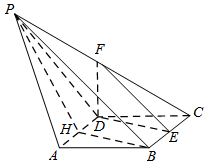$\because $ $PA = PD$，$\therefore $ $PH \perp AD$，$ AH = \dfrac{1}{2}$，$AB = 1$，$\angle DAB = 60^\circ $，
可得出 $BH = \dfrac{\sqrt 3 }{2}$，从而 ${AH}^2 + {BH}^2 = {AB}^2$，$\therefore $ $AH \perp HB$，
即 $AD \perp HB$，$\therefore $ $AD \perp 平面 PHB$，
又 $E$，$F$ 分别是 $BC$，$PC$ 的中点，$\therefore $ $EF\parallel PB$，
$\therefore $ $EF\parallel 平面 PHB$，又显然 $BH\parallel DE$，$\therefore $ $DE\parallel 平面 PHB$，
又 $DE$，$EF \subset 平面 DEF$，$DE \cap EF = E$，$\therefore $ 平面 $DEF\parallel 平面 PHB$，
$\because $ $AD \perp 平面 PHB$，$\therefore $ $AD \perp 平面 DEF$． -
求二面角 $P - AD - B$ 的余弦值．标注答案略解析由（1）知，$PH \perp AD$，$BH \perp AD$，且 $PH \subset 平面 PAD$，$BH \subset 平面 BAD$，
$\therefore $ $\angle PHB$ 就是二面角 $P - AD - B$ 的平面角，\[\begin{split}PH & = \sqrt {{{\left( {\sqrt 2 } \right)}^2} - {{\left( {\dfrac{1}{2}} \right)}^2}} = \dfrac{\sqrt 7 }{2}, \\ BH & = \dfrac{\sqrt 3 }{2}, \\ PB & = 2,\end{split}\]因此\[\begin{split} \cos \angle PHB & = \dfrac{{{PH}^2 + {BH}^2 - {PB}^2}}{2PH \cdot BH} \\ & = \dfrac{{\dfrac{7}{4} + \dfrac{3}{4} - 4}}{{2 \times \dfrac{\sqrt 7 }{2} \times \dfrac{\sqrt 3 }{2}}} \\ & = - \dfrac{{\sqrt {21} }}{7},\end{split} \]即二面角 $P - AD - B$ 的余弦值为 $ - \dfrac{{\sqrt {21} }}{7}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
