设圆 $C$ 与两圆 ${\left( {x + \sqrt 5 } \right)^2} + {y^2} = 4$，${\left( {x - \sqrt 5 } \right)^2} + {y^2} = 4$ 中的一个内切，另一个外切．
【难度】
【出处】
2011年高考广东卷（理）
【标注】
-
求 $C$ 的圆心轨迹 $L$ 的方程．标注答案略解析设 $F'\left( { - \sqrt 5 ,0} \right)$，$F\left( {\sqrt 5 ,0} \right)$，并设圆 $C$ 的半径为 $r$，则\[\left| {\left| {CF'} \right| - \left| {CF} \right|} \right| = \left| {\left( {2 + r} \right) - \left( {r - 2} \right)} \right| = 4,\]又 $4 < 2\sqrt 5 $，所以 $C$ 的圆心轨迹是以 $F'$，$F$ 为焦点的双曲线，且\[a = 2,c = \sqrt 5 ,\]从而\[b = 1,\]所以 $C$ 的圆心轨迹 $L$ 的方程为：\[\dfrac{{{x^2}}}{4} - {y^2} = 1.\]
-
已知点 $M\left( {\dfrac{{3\sqrt 5 }}{5},\dfrac{{4\sqrt 5 }}{5}} \right)$，$F\left( {\sqrt 5 ,0} \right)$，且 $P$ 为 $L$ 上动点，求 $\left| {\left| {MP} \right| - \left| {FP} \right|} \right|$ 的最大值及此时点 $P$ 的坐标．标注答案略解析如图，
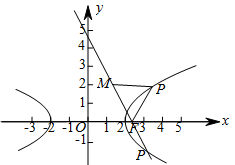\[\left| {\left| {MP} \right| - \left| {FP} \right|} \right| \leqslant \left| {MF} \right| = 2,\]等号当且仅当 $P$ 为直线 $MF$ 与双曲线的位于线段 $MF$ 的延长线上的那个交点处取得，直线 $MF$ 的方程为：\[2x + y - 2\sqrt 5 = 0,\]将直线方程代入双曲线方程中并整理得：\[\left( {3\sqrt 5 x - 14} \right)\left( {\sqrt 5 x - 6} \right) = 0,\]解得\[{x_1} = \dfrac{{14}}{{3\sqrt 5 }},{x_2} = \dfrac{6}{{\sqrt 5 }} = \dfrac{{18}}{{3\sqrt 5 }} > \dfrac{{14}}{{3\sqrt 5 }},\]所以 $P$ 点的横坐标应取 $\dfrac{6}{{\sqrt 5 }} = \dfrac{{6\sqrt 5 }}{5}$，代入得其纵坐标为 $ - \dfrac{{2\sqrt 5 }}{5}$，
综上所述，$\left| {\left| {MP} \right| - \left| {FP} \right|} \right|$ 的最大值为 $2$，此时点 $P$ 的坐标为 $\left( {\dfrac{{6\sqrt 5 }}{5}, - \dfrac{{2\sqrt 5 }}{5}} \right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
