查看数据源：59759dfb6b0745000a701c73
在直角坐标系 $xOy$ 中，曲线 $y=x^2+mx-2 $ 与 $x$ 轴交于 $A$，$B$ 两点，点 $ C $ 的坐标为 $(0,1)$，当 $m$ 变化时，解答下列问题：
【难度】
【出处】
2017年高考全国丙卷（文）
【标注】
  • 知识点
    >
    函数
    >
    根与系数的关系
    >
    二次方程的韦达定理
  • 知识点
    >
    平面几何
    >
    平面几何中的常用知识
    >
    圆幂定理
  1. 能否出现 $BC\perp AC$ 的情况？说明理由；
    标注
    • 知识点
      >
      函数
      >
      根与系数的关系
      >
      二次方程的韦达定理
    答案
    不可能出现，理由略
    解析
    若 $BC\perp AC$，根据射影定理，有\[OC^2=OA\cdot OB=1.\]而根据韦达定理，有\[OA\cdot OB=2,\]因此不可能出现 $BC\perp AC$ 的情况．
  2. 证明过 $A$，$B$，$C$ 三点的圆在 $y$ 轴上截得的弦长为定值．
    标注
    • 知识点
      >
      平面几何
      >
      平面几何中的常用知识
      >
      圆幂定理
    答案
    略
    解析
    如图，设 $D(0,-2)$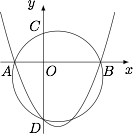．根据圆幂定理，有\[OA\cdot OB=OC\cdot OD=2,\]于是过 $A,B,C$ 三点的圆在 $y$ 轴截得的弦恒为 $CD$，其长度为定值 $3$．
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2
0.112344s