已知在椭圆 $\dfrac{x^2}4+\dfrac{y^2}3=1$ 上存在关于 $y=4x+m$ 对称的不同两点，求实数 $m$ 的取值范围．
【难度】
【出处】
2017年上海交通大学自主招生试题（回忆版）
【标注】
【答案】
$\left(-\dfrac{2\sqrt{13}}{13},\dfrac{2\sqrt{13}}{13}\right)$
【解析】
如图，设椭圆上两点 $A,B$ 关于直线 $l:y=4x+m$ 对称，$M$ 为线段 $AB$ 的中点，连接 $OM$．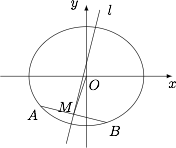
根据题意，直线 $AB$ 的斜率为 $-\dfrac 14$．由椭圆的垂径定理，可得直线 $OM$ 的斜率为 $3$．设 $M(t,3t)$，则 $m=-t$，又 $M$ 在椭圆内部，因此\[\dfrac{t^2}4+\dfrac{(3t)^2}3<1,\]解得 $m$ 的取值范围是 $\left(-\dfrac{2\sqrt{13}}{13},\dfrac{2\sqrt{13}}{13}\right)$．
根据题意，直线 $AB$ 的斜率为 $-\dfrac 14$．由椭圆的垂径定理，可得直线 $OM$ 的斜率为 $3$．设 $M(t,3t)$，则 $m=-t$，又 $M$ 在椭圆内部，因此\[\dfrac{t^2}4+\dfrac{(3t)^2}3<1,\]解得 $m$ 的取值范围是 $\left(-\dfrac{2\sqrt{13}}{13},\dfrac{2\sqrt{13}}{13}\right)$．
答案
解析
备注
