已知三棱锥 $SABC$ 的底面 $\triangle ABC$ 是等边三角形，$SA=2\sqrt 3$，其体积为 $\dfrac 94\sqrt 3$．已知点 $A$ 在面 $BCS$ 的投影是 $\triangle BCS$ 的垂心 $H$，求二面角 $H-AB-C$ 的大小．
【难度】
【出处】
2017年上海交通大学自主招生试题（回忆版）
【标注】
【答案】
$30^\circ$
【解析】
由于点 $A$ 在面 $BCS$ 上的投影为 $\triangle BCS$ 的垂心，四面体 $SABC$ 的三组对棱互相垂直，从而 $S$ 在面 $ABC$ 的投影为 $\triangle ABC$ 的中心 $O$，如图．可得 $H-AB-C=Q-AB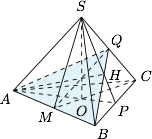-C$．
根据题意，可得 $SA=SB=SC=2\sqrt 3$，$AB=BC=CA=3$，进而可计算得 $Q-AB-C$ 的大小为 $30^\circ$．
根据题意，可得 $SA=SB=SC=2\sqrt 3$，$AB=BC=CA=3$，进而可计算得 $Q-AB-C$ 的大小为 $30^\circ$．
答案
解析
备注
