${F_1}, {F_2}$ 是椭圆 $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ 的焦点．
【难度】
【出处】
2006年北京大学自主招生保送生测试
【标注】
-
设 $l$ 是该椭圆的一条切线，${H_1},{H_2}$ 分别是 ${F_1},{F_2}$ 在 $l$ 上的垂足，证明：${F_1}{H_1} \cdot {F_2}{H_2} = {b^2}$．标注答案略解析设切点 $T\left( x_0, y_0 \right)$，则 $\dfrac{x_0^2}{a^2} + \dfrac{y_0^2}{b^2} = 1$，
$l:\dfrac{x_0x}{a^2} + \dfrac{y_0y}{b^2} = 1$，故\begin{align*}
F_1H_1\cdot F_2H_2
&=\dfrac{\left|\dfrac{-cx_0}{a^2}-1\right|}{\sqrt{\left(\dfrac{x_0}{a^2}\right)^2+\left(\dfrac{y_0}{b^2}\right)^2}}\cdot \dfrac{\left|\dfrac{cx_0}{a^2}-1\right|}{\sqrt{\left(\dfrac{x_0}{a^2}\right)^2+\left(\dfrac{y_0}{b^2}\right)^2}}\\
&=\dfrac{1-\dfrac{c^2x_0^2}{a^4}}{\dfrac{x_0^2}{a^4}+\dfrac{y_0^2}{b^4}}\\
&=\dfrac{a^4-c^2x_0^2}{x_0^2+\dfrac{a^4y_0^2}{b^4}}\\
&=b^2\cdot \dfrac{a^4-c^2x_0^2}{b^2x_0^2+a^4\cdot\dfrac{y_0^2}{b^2}}\\
&=b^2\cdot\dfrac{a^4+\left(b^2-a^2\right)x_0^2}{b^2x_0^2+a^4\left(1-\dfrac{x_0^2}{a^2}\right)}\\
&=b^2,
\end{align*}原命题得证． -
设 ${l_1},{l_2}$ 是该椭圆过椭圆外的一点 $P$ 的两条切线，切点分别为 ${T_1},{T_2}$，证明：$\angle {F_1}P{T_1} = \angle {F_2}P{T_2}$．标注答案略解析如图，作 ${F_1}$、${F_2}$ 分别关于切线 $P{T_1},P{T_2}$ 对称的点 $M,N$，则
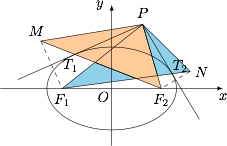因为 $PM = P{F_1}$，$P{F_2} = PN$，$M{F_2} = {F_1}N$ $ = 2a $（椭圆的光学性质），所以 $ \triangle PMF_{2}\cong\triangle PF_{1}N $．
于是 $ \angle MP{F_2} = \angle {F_1}PN $，从而 $ \angle MP{F_1} = \angle {F_2}PN $，也即 $ 2\angle {F_1}P{T_1} = 2\angle {F_2}P{T_2} $，因此 $ \angle {F_1}P{T_1} = \angle {F_2}P{T_2}$，原命题得证．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
