已知抛物线 $y = a{x^2}$,直线 ${l_1},{l_2}$ 都过点 $\left( {1, - 2} \right)$ 且互相垂直,若抛物线与直线 ${l_1},{l_2}$ 中至少一条相交,求 $a$ 的取值范围.
【难度】
【出处】
2006年复旦大学推优保送生考试(A卷)
【标注】
【答案】
$\left( { - \infty ,0} \right) \cup \left( {0,\dfrac{1}{8}} \right]$
【解析】
显然 $a \ne 0$.若 ${l_1},{l_2}$ 中有与 $y$ 轴平行的直线,那么无论 $a$ 取何值抛物线均符合题意.
因此以下讨论中均认为 ${l_1},{l_2}$ 斜率存在.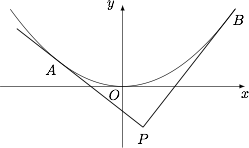
情形一 若 $a < 0$,则抛物线一定与两条直线中斜率为正的那条相交,符合题意;
情形二 若 $a > 0$,问题转化为过点 $P $ $\left( {1,- 2} \right) $ 作抛物线的两条切线 $ PA $、$ PB $,这两条切线对抛物线的张角 $ \theta $ 不小于 $ \dfrac{{\mathrm{\pi }}}{2} $.
设直线 $ y = k\left( {x - 1} \right) - 2 $ 与抛物线 $ y = a{x^2} $ 相切,则直线方程即\[kx - y - \left({k + 2} \right)= 0,\]抛物线方程即 $ {x^2} = \dfrac{1}{a}y$,它们相切的充要条件是\[ \dfrac{1}{{2a}}{k^2} = 2\left({k + 2} \right),\]即$$ {k^2} - 4ak - 8a = 0.$$而\[\theta \geqslant \dfrac{{\mathrm{\pi }}}{2} \Leftrightarrow - 1 \leqslant {k_1}{k_2} < 0 \Leftrightarrow - 1 \leqslant - 8a < 0\Leftrightarrow 0 < a \leqslant \dfrac{1}{8}.\]综合两种情形,$a$ 的取值范围为 $\left( { - \infty ,0} \right) \cup \left( {0,\dfrac{1}{8}} \right]$.
因此以下讨论中均认为 ${l_1},{l_2}$ 斜率存在.

设直线 $ y = k\left( {x - 1} \right) - 2 $ 与抛物线 $ y = a{x^2} $ 相切,则直线方程即\[kx - y - \left({k + 2} \right)= 0,\]抛物线方程即 $ {x^2} = \dfrac{1}{a}y$,它们相切的充要条件是\[ \dfrac{1}{{2a}}{k^2} = 2\left({k + 2} \right),\]即$$ {k^2} - 4ak - 8a = 0.$$而\[\theta \geqslant \dfrac{{\mathrm{\pi }}}{2} \Leftrightarrow - 1 \leqslant {k_1}{k_2} < 0 \Leftrightarrow - 1 \leqslant - 8a < 0\Leftrightarrow 0 < a \leqslant \dfrac{1}{8}.\]综合两种情形,$a$ 的取值范围为 $\left( { - \infty ,0} \right) \cup \left( {0,\dfrac{1}{8}} \right]$.
答案
解析
备注