如图，在四棱锥 $P - ABCD$ 中，$PA \perp 平面 ABCD$，底面 $ABCD$ 是菱形，$AB = 2$，$\angle BAD = {60^ \circ }$．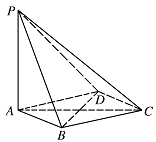
【难度】
【出处】
2011年高考北京卷（理）
【标注】
-
求证：$BD \perp $ 平面 $PAC $；标注答案略解析菱形对角线互相垂直为线面垂直的证明提供了一组垂直关系．因为四边形 $ ABCD $ 是菱形，所以 $ AC\perp BD $．
又因为 $ PA\perp 平面ABCD $，所以 $ PA\perp BD $．
所以 $ BD\perp 平面PAC $． -
若 $PA = AB $，求 $PB$ 与 $AC$ 所成角的余弦值；标注答案$ PB$ 与 $AC$ 所成角的余弦值为 $\dfrac{\sqrt 6 }{4}$解析合理地建立空间直角坐标系，利用空间向量进行解答即可．设 $ AC\cap BD=O $，因为\[ \angle BAD=60^\circ ,PA=AB=2,\]所以\[BO=1 ,AO=CO={\sqrt{3}}.\]如图，以 $ O $ 为坐标原点，建立空间直角坐标系 $ O-xyz $，
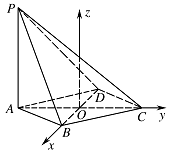则\[ P\left(0,-{\sqrt{3}},2\right),A\left(0,-{\sqrt{3}},0\right),B\left(1,0,0\right),C\left(0, {\sqrt{3}},0\right).\]所以\[{\overrightarrow {PB}}=\left(1, {\sqrt{3}},-2\right),{\overrightarrow {AC}}=\left(0,2{\sqrt{3}},0\right).\]设 $ PB $ 与 $ AC $ 所成角为 $ \theta $，则\[
\cos \theta = \dfrac{ {\overrightarrow {PB}} \cdot {\overrightarrow {AC}} }{ \left|{\overrightarrow {PB}} \right| \left|{\overrightarrow {AC}} \right| } ={\dfrac{6}{2{\sqrt{2}}\times 2{\sqrt{3}}}}={\dfrac{{\sqrt{6}}}{4}}. \]故 $ PB$ 与 $AC$ 所成角的余弦值为 $\dfrac{\sqrt 6 }{4}$． -
当平面 $PBC$ 与平面 $PDC$ 垂直时，求 $PA$ 的长．标注答案$ PA={\sqrt{6}} $解析可以利用空间向量的知识求解．由（2）知\[{\overrightarrow {BC}}=\left(-1, {\sqrt{3}},0\right).\]设 $ P\left(0,-{\sqrt{3}},t\right)\left(t>0\right) $，则\[{\overrightarrow {BP}}=\left(-1,-{\sqrt{3}},t\right).\]设平面 $ PBC $ 的法向量 $\overrightarrow m=\left(x,y,z\right) $，由\[\left\{ \begin{gathered}
\overrightarrow m \cdot \overrightarrow {BC} = 0, \\
\overrightarrow m \cdot \overrightarrow {BP} = 0, \\
\end{gathered} \right.\]得\[\left\{ \begin{gathered}- x + \sqrt 3 y = 0, \\
- x - \sqrt 3 y + tz = 0, \\
\end{gathered} \right.\]令 $ y={\sqrt{3}} $，则\[ \overrightarrow m=\left( 3, {\sqrt{3}},{\dfrac{6}{t}}\right) . \]同理，平面 $ PDC $ 的法向量\[\overrightarrow n= \left(-3, {\sqrt{3}},{\dfrac{6}{t}} \right).\]因为 $ 平面PBC\perp 平面PDC $，所以\[ \overrightarrow m \cdot \overrightarrow n=-6+{\dfrac{36}{t^2}}=0 ,\]解得\[ t={\sqrt{6}} ,\]所以 $ PA={\sqrt{6}} $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
