已知函数 $f\left(x\right) = A\sin \left(\dfrac{\mathrm \pi} {3}x + \varphi \right)$，$x \in {\mathbb {R}}$，$A > 0$，$0 < \varphi < \dfrac{\mathrm \pi} {2}$．$y = f\left(x\right)$ 的部分图象如图所示，$P,Q$ 分别为该图象的最高点和最低点，点 $P$ 的坐标为 $\left(1,A\right)$．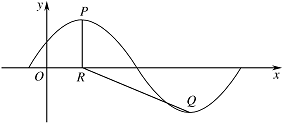
【难度】
【出处】
2011年高考浙江卷（文）
【标注】
-
求 $f\left(x\right)$ 的最小正周期及 $\varphi $ 的值；标注答案$T=6$，$\varphi = \dfrac{\mathrm \pi} {6}$解析由题意得，\[T = \dfrac{{2{\mathrm \pi} }}{{\dfrac{\mathrm \pi} {3}}} = 6.\]因为 $P\left(1,A\right)$ 在 $y = A\sin \left( {\dfrac{\mathrm \pi} {3}x + \varphi } \right)$ 的图象上，所以\[\sin \left( {\dfrac{\mathrm \pi} {3} + \varphi } \right) = 1.\]又因为 $0 < \varphi < \dfrac{\mathrm \pi} {2}$，所以\[\varphi = \dfrac{\mathrm \pi} {6}.\]
-
若点 $R$ 的坐标为 $\left( {1,0} \right)$，$\angle PRQ = \dfrac{{2{\mathrm \pi} }}{3}$，求 $A$ 的值．标注答案$A = \sqrt 3$解析设点 $Q$ 的坐标为 $\left( {{x_0},-A} \right)$．
由题意可知\[\dfrac{\mathrm \pi} {3}{x_0} + \dfrac{\mathrm \pi} {6} = \dfrac{{3{\mathrm \pi} }}{2},\]得\[{x_0} = 4,\]所以 $Q\left(4, - A\right)$．如图，连接 $PQ$，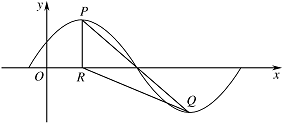
在 $\triangle PRQ$ 中，\[\angle PRQ = \dfrac{{2{\mathrm \pi} }}{3},\]由余弦定理得\[ \begin{split}\cos \angle PRQ & = \dfrac{{RP}^2 + {RQ}^2 - {PQ}^2}{2 RP \cdot RQ} \\& =\dfrac{A^2 + 9 + A^2 -\left(9+4A^2\right)}{2A \cdot \sqrt{9+A^2}} \\& = -\dfrac 1 2 .\end{split} \]解得 ${A^2} = 3$．又 $A > 0$，所以\[A = \sqrt 3 .\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
