如图，在三棱锥 $P - ABC$ 中，$AB = AC$，$D$ 为 $BC$ 的中点，$PO \perp 平面 ABC$，垂足 $O$ 落在线段 $AD$ 上．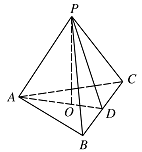
【难度】
【出处】
2011年高考浙江卷（文）
【标注】
-
证明：$AP \perp BC$；标注答案略解析由 $AB = AC$，$D$ 是 $BC$ 的中点，得 $AD \perp BC$，
又 $PO \perp 平面 ABC$，得 $PO \perp BC$．
因为 $PO \cap AD = O$，所以 $BC \perp 平面 PAD$，
故 $BC \perp PA$． -
已知 $BC = 8$，$PO = 4$，$AO = 3$，$OD = 2$．求二面角 $B - AP - C$ 的大小．标注答案略解析如图，在平面 $PAB$ 内作 $BM \perp PA$ 于 $M$，连接 $CM$．
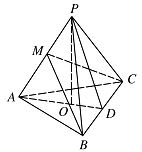因为 $BC \perp PA$，得 $AP \perp 平面 BMC$．所以 $AP \perp CM$．
故 $\angle BMC$ 为二面角 $B - AP - C$ 的平面角．
在 ${\mathrm{Rt}} \triangle ADB$ 中，${AB}^2 = {AD}^2 + {BD}^2 = 41$，得\[AB = \sqrt {41} ,\]在 $ {\mathrm{Rt }} \triangle POD$ 中，${PD}^2 = {PO}^2 + {OD}^2$，
在 $ {\mathrm{Rt}} \triangle PDB$ 中，${PB}^2 = {PD}^2 + {BD}^2$，
所以 ${PB}^2 = {PO}^2 + {OD}^2 + {BD}^2 = 36$，得\[PB = 6,\]在 ${\mathrm{Rt}} \triangle POA$ 中，${PA}^2 = {AO}^2 + {OP}^2 = 25$，得\[PA = 5.\]又\[\cos \angle BPA = \dfrac{{{PA}^2 + {PB}^2 - {AB}^2}}{2PA \cdot PB} = \dfrac{1}{3},\]从而 $\sin \angle BPA = \dfrac{2\sqrt 2 }{3}$，所以\[BM = PB\sin \angle BPA = 4\sqrt 2 .\]同理\[CM = 4\sqrt 2 .\]因为 ${BM}^2 + {MC}^2 = {BC}^2$，所以\[\angle BMC = {90^ \circ }.\]即二面角 $B - AP - C$ 的大小为 ${90^ \circ }$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
