如图,设 $P$ 为抛物线 ${C_1} : {x^2} = y$ 上的动点.过点 $P$ 作圆 ${C_2}:x^2+(y+3)^2=1$ 的两条切线,交直线 $l:y = - 3$ 于 $A$,$B$ 两点.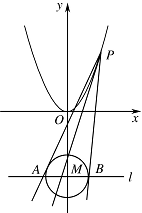

【难度】
【出处】
2011年高考浙江卷(文)
【标注】
-
求 ${C_2}$ 的圆心 $M$ 到抛物线 ${C_1}$ 准线的距离.标注答案略解析由题意可知,抛物线 ${C_1}$ 的准线方程为:\[y = - \dfrac{1}{4},\]所以圆心 $M$ 到抛物线 ${C_1}$ 准线的距离为\[\left| { - \dfrac{1}{4} - \left( - 3\right)} \right| = \dfrac{{11}}{4}.\]
-
是否存在点 $P$,使线段 $AB$ 被抛物线 ${C_1}$ 在点 $P$ 处得切线平分,若存在,求出点 $P$ 的坐标;若不存在,请说明理由.标注答案略解析设点 $P$ 的坐标为 $\left( {{x_0},x_0^2} \right)$,抛物线 ${C_1}$ 在点 $P$ 处的切线交直线 $l$ 于点 $D$.
再设 $A$,$B$,$D$ 的横坐标分别为 ${x_A}$,${x_B}$,${x_D}$.
过点 $P\left( {{x_0},x_0^2} \right)$ 的抛物线 ${C_1}$ 的切线方程为:\[y - {x_0^2} = 2{x_0}\left(x - {x_0}\right). \quad \cdots \cdots ① \]当 ${x_0} = 1$ 时,过点 $P\left( {1,1} \right)$ 与圆 ${C_2}$ 的切线 $PA$ 为:\[y - 1 = \dfrac{{15}}{8}\left(x - 1\right).\]可得\[{x_A} = \dfrac{{17}}{{15}},{x_B} = 1,{x_D} = - 1,\]因为 ${x_A} + {x_B} \ne 2{x_D}$,所以\[{x_0^2} - 1 \ne 0.\]设切线 $PA$,$PB$ 的斜率为 ${k_1}$,${k_2}$,则\[\begin{split}PA&:y - {x_0^2} = {k_1}\left(x - {x_0}\right), \quad \cdots \cdots ② \\ PB&:y - {x_0^2} = {k_2}\left(x - {x_0}\right), \quad \cdots \cdots ③ \end{split}\]将 $y = - 3$ 分别代入 ①,②,③,得\[\begin{split}{x_D} & = \dfrac{ {x_0^2} -3 }{2x_0}\left(x_0 \ne 0\right) , \\ {x_A} & =x_0 - \dfrac{ {x_0^2} +3 }{k_1} , \\ {x_B} & = x_0 - \dfrac{ {x_0^2} +3 }{k_2}\left(k_1,k_2 \ne 0\right) . \end{split} \]从而\[ {x_A} +{x_B} = 2x_0 - \left( {x_0^2} +3\right)\left(\dfrac 1 {k_1} +\dfrac 1 {k_2} \right).\]又 $\dfrac{{| - {x_0}{k_1} + x_0^2 + 3|}}{{\sqrt {k_1^2 + 1} }} = 1$,即\[\left(x_0^2 - 1\right)k_1^2 - 2\left(x_0^2 + 3\right){x_0}{k_1} + {\left(x_0^2 + 3\right)^2} - 1 = 0.\]同理\[\left(x_0^2 - 1\right)k_2^2 - 2\left(x_0^2 + 3\right){x_0}{k_2} + {\left(x_0^2 + 3\right)^2} - 1 = 0.\]所以 ${k_1},{k_2}$ 是方程 $\left(x_0^2 - 1\right){k^2} - 2\left(x_0^2 + 3\right){x_0}k + {\left(x_0^2 + 3\right)^2} - 1 = 0$ 的两个不相等的根,从而\[\begin{split}{k_1} + {k_2} & = \dfrac{{2{x_0}\left( {x_0^2 + 3} \right)}}{{x_0^2 - 1}}, \\ {k_1} \cdot {k_2} & = \dfrac{ \left( {x_0^2 + 3} \right)^2-1 }{{x_0^2 - 1}}.\end{split}\]因为 ${x_A} + {x_B} = 2{x_D}$,所以\[2{x_0} - \left( {3 + x_0^2} \right)\left( {\dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}}} \right) = \dfrac{{x_0^2 - 3}}{{{x_0}}},\]即 $\dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}} = \dfrac{1}{{{x_0}}}$.从而\[\dfrac{{2\left( {3 + x_0^2} \right){x_0}}}{{{{\left( {3 + x_0^2} \right)}^2}}} = \dfrac{1}{{{x_0}}},\]进而得 $x_0^4 = 8$,${x_0} = \pm \sqrt[4]{8}$.
综上所述,存在点 $P$ 满足题意,点 $P$ 的坐标为 $\left( { \pm \sqrt[4]{8},2\sqrt{2}} \right)$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2