如图，在三棱锥 $P - ABC$ 中，$ AB = AC $，$D$ 为 $BC$ 的中点，$PO \perp $ 平面 $ABC$，垂足 $O$ 落在线段 $AD$ 上，已知 $BC = 8$，$PO = 4$，$AO=3$，$OD = 2$．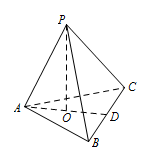
【难度】
【出处】
2011年高考浙江卷（理）
【标注】
-
证明：$AP \perp BC$；标注答案略解析如图，以 $O$ 为原点，以射线 $OP$ 为 $z$ 轴的正半轴，建立空间直角坐标系 $O-xyz$，
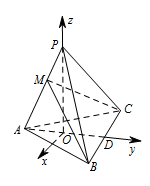则 $O\left( {0,0,0} \right)$，$A\left( {0, - 3,0} \right)$，$B\left( {4, 2,0} \right)$，$C\left( { - 4,2,0} \right)$，$P\left( {0,0,4} \right)$，$\overrightarrow {AP} = \left( 0,3,4\right)$，$ \overrightarrow {BC} = \left( - 8,0,0\right)$．
由此可得 $\overrightarrow {AP} \cdot \overrightarrow {BC} = 0$，所以 $\overrightarrow {AP} \perp \overrightarrow {BC} $，即 $AP \perp BC $． -
在线段 $ AP $ 上是否存在点 $M$，使得二面角 $A - MC - B$ 为直二面角？若存在，求出 $AM$ 的长；若不存在，请说明理由．标注答案略解析设 $\overrightarrow {PM} = \lambda \overrightarrow {PA} $，$\lambda \ne 1$，则 $\overrightarrow {PM} = \lambda \left(0, - 3, - 4\right) $，\[\overrightarrow {BM} = \overrightarrow {BP} + \overrightarrow {PM} = \overrightarrow {BP} + \lambda \overrightarrow {PA}
= \left( - 4 , - 2 - 3\lambda , 4 - 4\lambda \right) ,\]$ \overrightarrow {AC} = \left( - 4,5,0\right) ,\overrightarrow {BC} = \left( - 8,0,0\right) .$
设平面 $BMC$ 的法向量 $\overrightarrow {n_1} = \left( {x_1} , {y_1} , {z_1} \right)$，平面 $APC$ 的法向量 $\overrightarrow {n_2} = \left( {x_2} , {y_2} , {z_2} \right)$，
由 ${\begin{cases}
\overrightarrow {BM} \cdot \overrightarrow {n_1} = 0, \\
\overrightarrow {BC} \cdot \overrightarrow {n_1} = 0, \\
\end{cases}}$ 得\[{\begin{cases}- 4{x_1} - \left(2 + 3\lambda \right){y_1} + \left(4 - 4\lambda \right){z_1} = 0, \\
- 8{x_1} = 0, \\
\end{cases}}\]即\[\begin{cases}x_1 = 0,\\
z_1 = \dfrac{2 + 3\lambda }{4 - 4\lambda }y_1 ,
\end{cases} \]可取 $\overrightarrow {n_1} = \left( {0,1,\dfrac{2 + 3\lambda }{4 - 4\lambda }} \right)$，由 ${\begin{cases}\overrightarrow {AP} \cdot \overrightarrow {n_2} = 0, \\
\overrightarrow {AC} \cdot \overrightarrow {n_2} = 0, \\
\end{cases}}$ 即\[ \begin{cases}3y_2 + 4z_2 = 0, \\
- 4x_2 + 5y_2 = 0,
\end{cases} \]得\[{\begin{cases}{x_2} = \dfrac{5}{4}{y_2}, \\
{z_2} = - \dfrac{3}{4}{y_2}, \\
\end{cases}}\]可取 $\overrightarrow {n_2} = \left(5,4, - 3\right),$ 由 $\overrightarrow {n_1} \cdot \overrightarrow {n_2} = 0 $，得 $4 - 3 \cdot \dfrac{2 + 3\lambda }{4 - 4\lambda } = 0$，解得 $\lambda = \dfrac{2}{5},$ 故 $AM = 3 $．
综上所述，存在点 $M$ 符合题意，且 $AM = 3$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
