如图,在 $\triangle ABC$ 中,$\angle ABC = {45^ \circ }$,$\angle BAC = {90^ \circ }$,$AD$ 是 $BC$ 上的高,沿 $AD$ 把 $\triangle ABD$ 折起,使 $\angle BDC = {90^ \circ }$.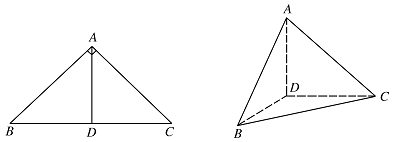

【难度】
【出处】
2011年高考陕西卷(文)
【标注】
-
证明:平面 $ADB \perp 平面 BDC$;标注答案略解析$\because$ 折起前 $AD$ 是 $BC$ 边上的高,
$\therefore$ 当 $\triangle ABD$ 折起后,$AD \perp DC$,$AD \perp DB$,
又 $DB \cap DC = D$,$\therefore$ $AD \perp 平面 BDC$.
又 $\because$ $AD \subset 平面 ABD$.
$\therefore$ 平面 $ABD \perp 平面 BDC$. -
设 $BD = 1$,求三棱锥 $D - ABC$ 的表面积.标注答案略解析由(1)知,$DA \perp DB$,$DB \perp DC$,$DC \perp DA$.
因为 $DB = DA = DC = 1$,所以\[AB = BC = CA = \sqrt 2,\]从而\[\begin{split}{S_{\triangle DAB}} & = {S_{\triangle DBC}} \\& = {S_{\triangle DCA}} \\& = \dfrac{1}{2} \times 1 \times 1 \\& = \dfrac{1}{2}, \\ {S_{\triangle ABC}} & = \dfrac{1}{2} \times \sqrt 2 \times \sqrt 2 \times \sin 60^\circ \\& = \dfrac{\sqrt 3 }{2},\end{split}\]所以表面积\[S = \dfrac{1}{2} \times 3 + \dfrac{\sqrt 3 }{2} = \dfrac{3 + \sqrt 3 }{2}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2