如图，在 $\triangle ABC$ 中，$\angle ABC = 60^\circ $，$\angle BAC = 90^\circ $，$AD$ 是 $BC$ 上的高，沿 $AD$ 把 $\triangle ABD$ 折起，使 $\angle BDC = 90^\circ $．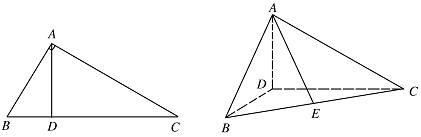
【难度】
【出处】
2011年高考陕西卷（理）
【标注】
-
证明：平面 $ADB \perp $ 平面 $BDC$；标注答案略解析$\because$ 折起前 $AD$ 是 $BC$ 边上的高，
$\therefore$ 当 $\triangle ABD$ 折起后，$AD \perp DC$，$AD \perp DB$．
又 $DB \cap DC = D$，$\therefore$ $AD \perp $ 平面 $BDC$．
$\because$ $AD$ $ \subset $ 平面 $ABD$，$\therefore$ 平面 $ABD \perp $ 平面 $BDC $． -
设 $E$ 为 $BC$ 的中点，求 $\overrightarrow {AE} $ 与 $\overrightarrow {DB} $ 夹角的余弦值．标注答案$\dfrac{{\sqrt {22} }}{22}$解析由 $\angle BDC = {90^ \circ }$ 及（1）知 $DA$，$DB$，$DC$ 两两垂直，
不妨设 $\left| {DB} \right| = 1$，以 $D$ 为坐标原点，以 $\overrightarrow {DB} $，$\overrightarrow {DC} $，$\overrightarrow {DA} $ 所在直线为 $x$，$y$，$z$ 轴建立如图所示的空间直角坐标系，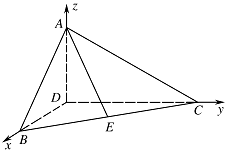
易得：$D\left( {0,0,0} \right)$，$B\left( {1,0,0} \right)$，$C\left( {0,3,0} \right)$，$A\left( {0,0,\sqrt 3 } \right)$，$E\left( {\dfrac{1}{2},\dfrac{3}{2},0} \right)$，
所以\[ \begin{split}\overrightarrow {AE} &= \left( {\dfrac{1}{2},\dfrac{3}{2}, - \sqrt 3 } \right), \\ \overrightarrow {DB} &= \left(1,0,0\right),\end{split} \]所以\[ \begin{split}\cos \left\langle {\overrightarrow {AE} ,\overrightarrow {DB} } \right\rangle & = \dfrac{{\overrightarrow {AE} \cdot \overrightarrow {DB} }}{{\left| {\overrightarrow {AE} } \right| \cdot \left| {\overrightarrow {DB} } \right|}} \\& = \dfrac{{\dfrac{1}{2}}}{{1 \times \sqrt {\dfrac{22}{4}} }} = \dfrac{{\sqrt {22} }}{22},\end{split} \]所以 $\overrightarrow {AE} $ 与 $\overrightarrow {DB} $ 夹角的余弦值是 $\dfrac{{\sqrt {22} }}{22}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
