如图,设 $P$ 是圆 ${x^2} + {y^2} = 25$ 上的动点,点 $D$ 是 $P$ 在 $x$ 轴上的投影,$M$ 为 $PD$ 上一点,且 $\left| {MD} \right| = \dfrac{4}{5}\left| {PD} \right|$.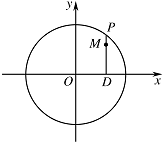

【难度】
【出处】
2011年高考陕西卷(理)
【标注】
-
当 $P$ 在圆上运动时,求点 $M$ 的轨迹 $C$ 的方程;标注答案略解析设点 $M$ 的坐标是 $\left( {x,y} \right)$,$P$ 的坐标是 $\left({x_p},{y_p}\right)$,
则根据题意得\[{x_p} = x,{y_p} = \dfrac{5}{4}y,\]因为点 $P $ 在圆 ${x^2} + {y^2} = 25$ 上,所以\[{x^2} + {\left( {\dfrac{5}{4}y} \right)^2} = 25,\]整理即得轨迹 $C $ 的方程为\[\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{{16}} = 1.\] -
求过点 $\left(3,0\right)$ 且斜率为 $\dfrac{4}{5}$ 的直线被 $C$ 所截线段的长度.标注答案略解析过点 $\left(3.0\right)$ 且斜率为 $\dfrac{4}{5}$ 的直线方程是\[y = \dfrac{4}{5}\left(x - 3\right),\]设此直线与 $C$ 的交点为 $A\left({x_1},{y_1}\right)$,$B\left({x_2},{y_2}\right)$,将 $y = \dfrac{4}{5}\left(x - 3\right)$ 代入 轨迹 $C$ 的方程得\[\dfrac{{{x^2}}}{{25}} + \dfrac{{{{\left(x - 3\right)}^2}}}{{25}} = 1,\]化简得\[{x^2} - 3x - 8 = 0,\]解得\[\begin{split}{x_1} &= \dfrac{{3 - \sqrt {41} }}{2} , \\ {x_2} &= \dfrac{{3 + \sqrt {41} }}{2},\end{split}\]所以线段 $AB$ 的长度是\[\begin{split}\left| {AB} \right|&{\text{ = }}\sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} \\& = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + \dfrac{{16}}{{25}}{{\left( {{x_1} - {x_2}} \right)}^2}}\\& = \sqrt {\left( {1 + \frac{{16}}{{25}}} \right){{\left( {{x_1} - {x_2}} \right)}^2}}\\& = \sqrt {\frac{{41}}{{25}} \times 41} = \frac{{41}}{5}.\end{split}\]故所截线段的长度是 $\dfrac{{41}}{5}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2