在一个棱长为 $1$ 的正方体中,设 $V_1$ 是以各面中心为顶点的小几何体的体积,$V_2$ 是以这个小几何体各面中心为顶点的更小几何体的体积,求 $V_1$ 和 $V_2$ 的值.
【难度】
【出处】
2008年第十九届“希望杯”全国数学邀请赛高一(二试)
【标注】
【答案】
$V_1=\dfrac 16$,$V_2=\dfrac {1}{27}$
【解析】
如图,正方体 $ABCD-A_1B_1C_1D_1$ 的棱长为 $1$,$E,F,G,H,M,N$ 分别是各面中心,连接 $MN$,则$$V_1=\dfrac 13 MN \cdot S_{EFGH}=\dfrac 16.$$进而 $V_2$ 是一个棱长为 $\dfrac 13$ 的小正方体的体积,所以\[V_2=\dfrac {1}{27}.\]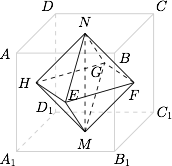

答案
解析
备注