如图,某市在海岛 $A$ 上建了一水产养殖中心.在海岸线上有相距 $70$ 公里的 $B,C$ 两个小镇,并且 $AB=30$ 公里,$AC=80$ 公里,已知 $B$ 镇在养殖中心工作的员工有 $3$ 百人,$C$ 镇在养殖中心工作的员工有 $5$ 百人.现欲在 $BC$ 之间建一个码头 $D$,运送来自两镇的员工到养殖中心工作,又知水路运输与陆路运输每百人每公里运输成本之比为 $1:2$.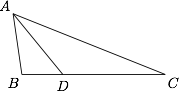

【难度】
【出处】
无
【标注】
-
求 $\sin\angle ABC$ 的大小;标注答案$\sin\angle ABC=\dfrac{4\sqrt 3}7$解析根据余弦定理,有\[\cos\angle ABC=\dfrac{AB^2+BC^2-AC^2}{2\cdot AB\cdot BC}=-\dfrac 17,\]于是\[\sin\angle ABC=\dfrac{4\sqrt 3}7.\]
-
设 $\angle ADB=\theta$,试确定 $\theta$ 的大小,使得运输总成本最少.标注答案略解析不妨设水路运输成本为 $m$ 元 每百人每公里,陆路运输成本为 $2m$ 元每百人每公里,则总成本\[p=8AD\cdot m+(3BD+5CD)\cdot 2m=(700+8AD-4BD)\cdot m.\]在 $\triangle ABD$ 中应用正弦定理,有\[\dfrac{AB}{\sin\theta}=\dfrac{AD}{\sin\angle ABC}=\dfrac{BD}{\sin\left(\theta+\angle ABC\right)},\]解得\[AD=\dfrac{120\sqrt 3}{7\sin\theta},BD=\dfrac{120\sqrt 3\cos\theta}{7\sin\theta}-\dfrac{30}7,\]因此\[2AD-BD=\dfrac{120\sqrt 3}{7}\cdot \dfrac{2-\cos\theta}{\sin\theta}+\dfrac{30}7,\]设\[y=\dfrac{2-\cos\theta}{\sin \theta},\]则\[y\sin\theta+\cos\theta=2,\]于是\[\dfrac{2}{\sqrt{y^2+1}}\leqslant 1,\]解得 $y\geqslant \sqrt 3$,且 $\theta=\dfrac{\pi}3$ 时取得等号.
因此当 $\theta=\dfrac{\pi}3$ 时,运输总成本最小.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2