椭圆 $E $ 经过点 $A\left(2,3\right) $,对称轴为坐标轴,焦点 $ F_1$,$ F_2$ 在 $ x$ 轴上,离心率 $e=\dfrac12 $.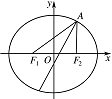

【难度】
【出处】
2010年高考安徽卷(文)
【标注】
-
求椭圆 $E $ 的方程;标注答案略解析设椭圆 $ E $ 的方程为 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 $ $\left(a>b>0\right) $.
由 $ e=\dfrac12$,得\[\dfrac ca=\dfrac12,b^2=a^2-c^2=3c^2,\]所以\[\dfrac{x^2}{4c^2}+\dfrac{y^2}{3c^2}=1,\]将 $A\left(2,3\right)$ 代入,有\[\dfrac1{c^2}+\dfrac3{c^2}=1,\]解得\[c=2,\]所以椭圆 $E$ 的方程为\[\dfrac{x^2}{16}+\dfrac{y^2}{12}=1.\] -
求 $\angle F_1AF_2 $ 的角平分线所在直线的方程.标注答案略解析由(1)知 $ {F_1}\left( - 2,0\right) $,$ {F_2}\left(2,0\right) $,所以直线 $ A{F_1} $ 的方程为\[ y = \dfrac{3}{4}\left(x + 2\right) ,\]即\[ 3x - 4y + 6 = 0. \]直线 $ A{F_2} $ 的方程为 $ x =2 $.
由椭圆 $ E $ 的图形知,$ \angle {F_1}A{F_2} $ 的角平分线所在直线的斜率为正数.
设 $ P\left(x,y\right) $ 为 $ \angle {F_1}A{F_2} $ 的角平分线所在直线上任一点,则有\[ \dfrac{|3x-4y+6|}5=|x-2| .\]若 $ 3x - 4y + 6 = 5x - 10 $,得\[ x + 2y - 8 = 0, \]其斜率为负,不合题意,舍去.于是\[ 3x - 4y + 6 = - 5x + 10,\]即\[ 2x - y - 1 = 0. \]所以 $ \angle {F_1}A{F_2} $ 的角平分线所在直线的方程为\[ 2x - y - 1 = 0. \]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2