设 ${C_1}$,${C_2}$,$ \cdots$,${C_n}$,$ \cdots $ 是坐标平面上的一列圆,它们的圆心都在 $x$ 轴的正半轴上,且都与直线 $y = \dfrac{\sqrt 3 }{3}x$ 相切,对每一个正整数 $n$,圆 ${C_n}$ 都与圆 ${C_{n + 1}}$ 相互外切,以 ${r_n}$ 表示 ${C_n}$ 的半径,已知 $\left\{ {r_n}\right\} $ 为递增数列.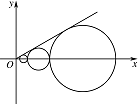

【难度】
【出处】
2010年高考安徽卷(文)
【标注】
-
证明:$\left\{ {r_n}\right\} $ 为等比数列;标注答案略解析将直线 $ y = \dfrac{\sqrt 3 }{3}x $ 的倾斜角记为 $\theta $,则有\[ \tan \theta = \dfrac{\sqrt 3 }{3},\sin \theta = \dfrac{1}{2}, \]设 $ C_n$ 的圆心为 $ \left(\lambda _n,0\right) $,则由题意得知 $ \dfrac{ r _n}{\lambda _n }= \dfrac{1}{2} $,得\[ \lambda _n = 2r_n ;\]同理 $ \lambda _{n + 1}= 2r_{n + 1} $,从而\[ \lambda _{n + 1} = \lambda _{n}+ r_n+ r_ {n + 1} = 2r_ {n + 1},\]将 $\lambda _n= 2r_n$ 代入,解得\[r_ {n + 1} = 3r_n ,\]故 $ \left\{r_n\right\}$ 为公比 $ q = 3 $ 的等比数列.
-
设 ${r_1} = 1$,求数列 $\left\{ \dfrac{n}{r_n}\right\} $ 的前 $n$ 项和.标注答案略解析由于 $r_1 = 1 $,$ q = 3 $,故 $r_n = 3^{n - 1}$,从而\[ \dfrac n{r_n} = n3^{1 - n} ,\]记\[ S_n = \dfrac{1}{r_1 } + \dfrac{2}{ r _2 } +\cdots + \dfrac{n} {r _n},\]则有\[ \begin{split}S_n &= 1 + 2\times {3^{ - 1}} + 3\times {3^{ - 2}} + \cdots +n{3^{1 - n}} ,&\quad \cdots \cdots ① \\ \dfrac{S_n}{3} &= 1\times {3^{ - 1}} + 2\times {3^{ - 2}} + \cdots+ \left(n - 1\right){3^{1 - n}} + n{3^{ - n}}, &\quad \cdots \cdots ② \end{split} \]$ ① - ② $,得\[ \begin{split}\dfrac{2{S_n}}{3} &= 1 + {3^{ - 1}} + {3^{ - 2}} + \cdots + {3^{1 - n}} - n{3^{ - n}} \\&= \dfrac{{1 - {3^{ - n}}}}{{\frac{2}{3}}} - n{3^{ - n}} \\&= \dfrac{3}{2} - \left(n + \dfrac{3}{2}\right){3^{ - n}},\end{split} \]所以\[ {S_n} = \dfrac{9}{4} - \dfrac{1}{2}\left(n + \dfrac{3}{2}\right){3^{1 - n}} = \dfrac{{9 - \left(2n + 3\right){3^{1 - n}}}}{4} .\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2