如图，在多面体 $ ABCDEF $ 中，四边形 $ ABCD $ 是正方形，$ AB=2EF=2 $，$ EF\parallel AB $，$ EF\perp FB $，$ \angle BFC=90^\circ $，$ BF=FC $，$ H $ 为 $ BC $ 的中点．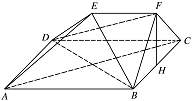
【难度】
【出处】
2010年高考安徽卷（文）
【标注】
-
求证：$ FH\parallel 平面 EDB $；标注答案略解析如图，设 $ AC $ 与 $ BD $ 交于点 $ G $，则 $ G $ 为 $ AC $ 的中点，连接 $ EG $，$ GH $．
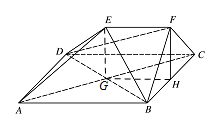由于 $ H $ 为 $ BC $ 的中点，故 $ GH \parallel AB $，$ GH= \dfrac{1}{2}AB $．
又 $ EF \parallel AB $，$ EF =\dfrac{1}{2}AB $，$ \therefore $ 四边形 $ EFHG $ 为平行四边形，
$\therefore$ $ EG\parallel FH $，而 $ EG \subset 平面 EDB $，$FH\not\subset 平面 EDB $，
$\therefore$ $ FH\parallel 平面 EDB $． -
求证：$ AC\perp 平面 EDB $；标注答案略解析由四边形 $ ABCD $ 为正方形，有 $ AB \perp BC $．
又 $ EF\parallel AB $，$\therefore$ $ EF \perp BC $．
而 $ EF \perp FB $，$\therefore$ $ EF \perp 平面 BFC $，
$\therefore$ $ EF \perp FH $，$\therefore$ $ AB \perp FH $．
又 $ BF = FC $，$ H $ 为 $ BC $ 的中点，
$\therefore$ $ FH \perp BC $．$\therefore$ $ FH \perp 平面 ABCD $．
$\therefore$ $ FH \perp AC $．
又 $ FH\parallel EG $，$\therefore$ $ AC \perp EG $，
又 $ AC \perp BD $，$ EG \cap BD = G $，
$\therefore$ $ AC \perp 平面 EDB $． -
求四面体 $ B-DEF $ 的体积．标注答案略解析$\because$ $ EF \perp FB $，$ \angle BFC = {90^\circ} $，$\therefore$ $ BF \perp 平面 CDEF $．
$\therefore$ $ BF $ 为四面体 $ B - DEF $ 的高．
又 $ BC = AB = 2 $，$\therefore$ $ BF = FC = \sqrt 2 $，所以\[{V_{B - DEF}} = \dfrac{1}{3} \times \dfrac{1}{2} \times 1 \times \sqrt 2 \times \sqrt 2 = \dfrac{1}{3}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
