如图,已知椭圆 $ E $ 经过点 $ A\left(2,3\right) $,对称轴为坐标轴,焦点 $ F_{1} $,$ F_{2} $ 在 $ x $ 轴上,离心率 $e = \dfrac{1}{2}$.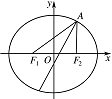

【难度】
【出处】
2010年高考安徽卷(理)
【标注】
-
求椭圆 $ E $ 的方程;标注答案略解析设椭圆 $ E $ 的方程为 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 $.
由 $ e=\dfrac12$,得\[\dfrac ca=\dfrac12,b^2=a^2-c^2=3c^2,\]所以\[\dfrac{x^2}{4c^2}+\dfrac{y^2}{3c^2}=1,\]将 $A\left(2,3\right)$ 代入,有\[\dfrac1{c^2}+\dfrac3{c^2}=1,\]解得 $c=2$,所以椭圆 $E$ 的方程为 $\dfrac{x^2}{16}+\dfrac{y^2}{12}=1$. -
求 $\angle {F_1}A{F_2}$ 的角平分线所在直线 $l$ 的方程;标注答案略解析解法一:由(1)知 $ {F_1}\left( - 2,0\right) $,$ {F_2}\left(2,0\right) $,所以直线 $ A{F_1} $ 的方程为\[ y = \dfrac{3}{4}\left(x + 2\right) ,\]即\[ 3x - 4y + 6 = 0. \]直线 $ A{F_2} $ 的方程为 $ x =2 $.
由椭圆 $ E $ 的图形知,$ \angle {F_1}A{F_2} $ 的角平分线所在直线的斜率为正数.
设 $ P\left(x,y\right) $ 为 $ \angle {F_1}A{F_2} $ 的角平分线所在直线上任一点,则有\[ \dfrac{|3x-4y+6|}5=|x-2| .\]若 $ 3x - 4y + 6 = 5x - 10 $,得\[ x + 2y - 8 = 0, \]其斜率为负,不合题意,舍去.于是\[ 3x - 4y + 6 = - 5x + 10,\]即\[ 2x - y - 1 = 0. \]所以 $ \angle {F_1}A{F_2} $ 的角平分线所在直线的方程为 $2x - y - 1 = 0$.
解法二:因为 $ A\left(2,3\right)$,${F_1}\left( - 2,0\right)$,${F_2}\left(2,0\right)$,
所以\[ \overrightarrow {A{F_1}} = \left( - 4, - 3\right),\overrightarrow {A{F_2}} = \left(0, - 3\right),\]所以\[\dfrac{{\overrightarrow {A{F_1}} }}{{ \left|\overrightarrow {A{F_1}} \right|}} + \dfrac{{\overrightarrow {A{F_2}} }}{{ \left|\overrightarrow {A{F_2}} \right|}} = \dfrac{1}{5}\left( - 4, - 3\right) + \dfrac{1}{3}\left(0, - 3\right) = - \dfrac{4}{5}\left(1,2\right).\]所以 $ {k_1} = 2 $,所以\[ l:y - 3 = 2\left(x - 1\right),\]即\[2x - y - 1 = 0. \] -
在椭圆 $ E $ 上是否存在关于直线 $l$ 对称的相异两点?若存在,请找出;若不存在,说明理由.标注答案略解析解法一:假设存在这样的两个不同的点 $B\left({x_1},{y_1}\right)$ 和 $C\left({x_2},{y_2}\right)$.
因为 $ BC \perp l $,所以\[{k_{BC}} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \dfrac{1}{2}. \]设 $ BC $ 的中点为 $ M\left({x_0},{y_0}\right) $,则\[ {x_0} = \dfrac{{{x_1} + {x_2}}}{2},{y_0} = \dfrac{{{y_1} + {y_2}}}{2}, \]由于 $ M $ 在 $ l $ 上,故\[2{x_0} - {y_0} + 1 = 0. \quad \cdots \cdots ① \]又 $ B $,$ C $ 在椭圆上,所以有\[\dfrac{{x_1^2}}{{16}} + \dfrac{{y_1^2}}{{12}} = 1 与 \dfrac{{x_2^2}}{{16}} + \dfrac{{y_2^2}}{{12}} = 1.\]两式相减,得\[\dfrac{x^2_2-x^2_1}{16}+\dfrac{y^2_2-y^2_1}{12}=0,\]即\[\dfrac{\left(x_1+x_2\right)\left(x_2-x_1\right)}{16}+\dfrac{\left(y_1+y_2\right)\left(y_2-y_1\right)}{12}=0.\]将该式写为\[\dfrac{1}{8} \cdot \dfrac{{{x_1} + {x_2}}}{2} + \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} \cdot \dfrac{1}{6} \cdot \dfrac{{{y_1} + {y_2}}}{2} = 0,\]并将直线 $ BC $ 的斜率 ${k_{BC}}$ 和线段 $ BC $ 的中点,表示代入该表达式中,得\[\dfrac{1}{8}{x_0} - \dfrac{1}{{12}}{y_0} = 0,\]即\[3{x_0} - 2{y_0} = 0. \quad \cdots \cdots ② \]$ ① \times 2- ② $ 得\[{x_2} = 2,{y_0} = 3,\]即 $ BC $ 的中点为点 $ A $,而这是不可能的.所以 不存在满足题设条件的点 $ B $ 和 $ C $.
解法二:
假设存在 $B\left({x_1},{y_1}\right)$,$C\left({x_2},{y_2}\right)$ 两点关于直线 $ l $ 对称,
则 $l \perp BC$,所以 $ {k_{BC}} = - \dfrac{1}{2}$,设直线 $ BC $ 的方程为\[ y = - \dfrac{1}{2}x + m ,\]将其代入椭圆方程\[ \dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{{12}} = 1 ,\]得一元二次方程\[3{x^2} + 4{\left( - \dfrac{1}{2}x + m\right)^2} = 48,\]即\[{x^2} - mx + {m^2} - 12 = 0,\]则 ${x_1}$ 与 $ {x_2}$ 是该方程的两个根,由韦达定理得\[{x_1} + {x_2} = m,\]于是\[{y_1} + {y_2} = - \dfrac{1}{2}\left({x_1} + {x_2}\right) + 2m = \dfrac{{3m}}{2},\]所以 $ B $,$ C $ 的中点坐标为 $\left(\dfrac{m}{2},\dfrac{{3m}}{4}\right).$
又线段 $ BC $ 的中点在直线 $y = 2x - 1$ 上,所以 $\dfrac{{3m}}{4} = m - 1$,得 $m = 4$.
即 $ B $,$ C $ 的中点坐标为 $ \left(2,3\right) $,与点 $ A $ 重合,矛盾.
所以 不存在满足题设条件的相异两点.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3